Question

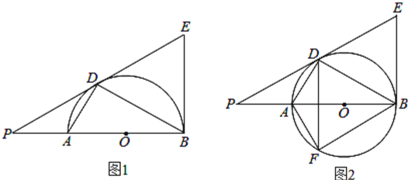
【题目】如图，AB是⊙O的直径，点C是弧BE中点，AE⊥CD于点D，延长DC，AB交于点F，已知AD＝4，FC＝FB．

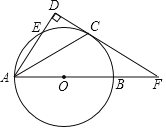
（1）求证：CD是⊙O的切线．

（2）求线段FC的长．

Answer 1

【答案】（1）见解析；（2）FC＝6．

【解析】

（1）连接OC，由等腰三角形的性质和角平分线的定义得出∠DAC=∠OCA，于是可判断OC∥AD，由于AD⊥CD，则OC⊥CD，然后根据切线的判定定理即可得到结论；

（2）有了FC=FB，设BF=x，则CF=x，根据切割线定理得到,设OA=OB=OC=r，求得BF=2r，根据相似三角形的性质得到BF=6，于是得到结论．

（1）证明：连接OC．

∵C是的中点，

∴AC平分∠DAB，

∴∠DAC＝∠OAC，

∵OA＝OC，

∴∠OCA＝∠OAC，

∴∠DAC＝∠OCA，

∴DA∥OC，

∵AD⊥DC，

∴∠ADC＝90°，

∴∠OCD＝90°，

即OC⊥DC，

∵OC为半径，

∴DC为⊙O的切线；

（2）∵FC＝FB，

∴设BF＝x，则CF＝x，

∵CD是⊙O的切线，

∴CF2＝BFAF，

设OA＝OC＝OB＝r，

∴2x2＝x（x+2r），

∴x＝2r，

∴BF＝2r，

∵OC∥AD，

∴△OCF∽△ADF，

∴，

∴ ，

∴r＝3，

∴BF＝6，

∴FC＝FB＝6．