题目内容
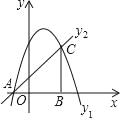
【题目】已知抛物线![]() 过点A(m-2,n), B(m+4,n),C(m,
过点A(m-2,n), B(m+4,n),C(m,![]() ).
).
(1)b=__________(用含m的代数式表示);
(2)求△ABC的面积;
(3)当![]() 时,均有
时,均有![]() ,求m的值.
,求m的值.
【答案】(1)b=-2m-2;(2)24;(3)![]() .
.
【解析】
(1)根据A(m-2,n), B(m+4,n)纵坐标一致,结合对称轴即可求解;
(2)先用含m的代数式表示c,再带入A点坐标即可求出n=3,最后利用铅锤法即可求出△ABC的面积;
(3)先用只含m的代数式表示二次函数解析式,再结合带取值范围的二次函数最值求法分类讨论即可.
(1)∵![]() 过点A(m-2,n), B(m+4,n),
过点A(m-2,n), B(m+4,n),
∴对称轴![]()
∴![]()
(2)∵![]()
∴![]()
把C(m,![]() )代入
)代入![]()
∴![]()
∴![]()
把A(m-2,n)代入![]()
得![]()
∴n=3
∴A(m-2,3), B(m+4,3),C(m,![]() )
)
∴AB=6
C点到x轴的距离为:3﹣(-5)=8,
∴S△ABC=![]() ×6×8=24
×6×8=24
(3)∵n=3
∴![]()
∴![]()
∴当![]() 时
时
![]()
∵![]()
∴由函数增减性知![]()
即![]()
∴当![]() 时
时
由函数增减性知![]() 时,
时,![]()
∴![]()
∴![]() (舍)
(舍)
当![]() 时
时
由函数增减性知![]() 时,
时,![]()
∴![]()
∴![]() (舍)
(舍)![]()
∴![]()

【题目】“停课不停学,学习不延期”,某市通过教育资源公共服务平台和有线电视为全市中小学开设在线“空中课堂”,为了解学生每天的学习时间情况,在全市随机抽取了部分初中学生进行问卷调查,现将调查结果绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题:
组别 | 学习时间x(h) | 人数(人) |
A | 2.5<x≤3 | 40 |
B | 3<x≤3.5 | 170 |
C | 3.5<x≤4 | 350 |
D | 4<x≤4.5 | |
E | 4.5<x≤5 | 90 |
F | 5小时以上 | 50 |
表1
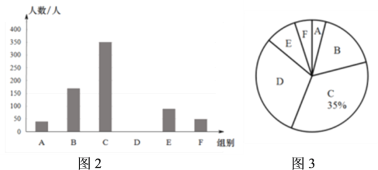
(1)这次参与问卷调查的初中学生有 人,中位数落在 组.
(2)图3中D组对应的角度是 ,并补全图2 条形统计图.
(3)若某市有初中学生2.8万人,请估计每天参与“空中课堂”学习时间3.5到4.5小时(不包括3.5小时)的初中学生有多少人?