题目内容
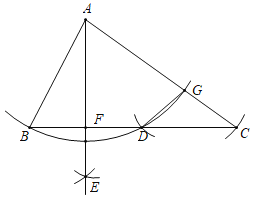
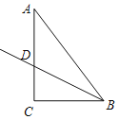
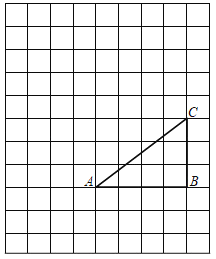
【题目】如图,将△ABC放在每个小正方形的边长为1的网格中,点A、B、C均在格点上.
(1)边AC的长等于_____.
(2)以点C为旋转中心,把△ABC顺时针旋转,得到△A'B'C',使点B的对应点B'恰好落在边AC上,请在如图所示的网格中,用无刻度的直尺,作出旋转后的图形,并简要说明作图的方法(不要求证明).
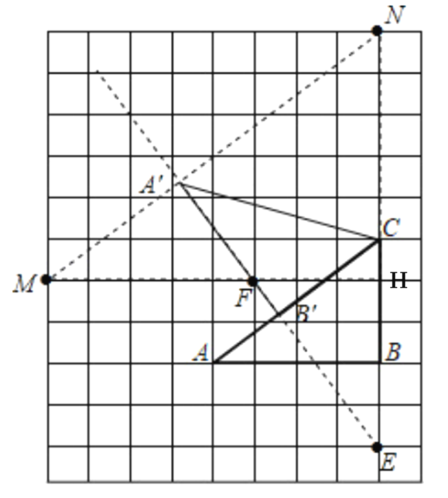
【答案】(1)5;(2)取格点E,F,M,N,作直线EF,直线MN,MN与EF交于点A′,EF与AC交于点B′,连接CA′.△A'B'C即为所求.作图见解析.
【解析】
(1)先根据网格确定AB、BC的长,然后根据勾股定理即可解答;
(2)利用格点构造全等三角形CB'=FH=3,EF⊥AC, A'B'=4,从而点E、F、M、N,作直线EF,直线MN,MN与EF交于点A',EF与AC交于点B',连接CA'即可.
解:(1)根据网格可知:
AB=4,BC=3,
∴AC=![]() =5,
=5,
故答案为:5;
(2)取格点E,F,M,N,作直线EF,直线MN,
MN与EF交于点A′,
EF与AC交于点B′,
连接CA′.
△A'B'C即为所求.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案【题目】“停课不停学,学习不延期”,某市通过教育资源公共服务平台和有线电视为全市中小学开设在线“空中课堂”,为了解学生每天的学习时间情况,在全市随机抽取了部分初中学生进行问卷调查,现将调查结果绘制成如下不完整的统计图表,请根据图表中的信息解答下列问题:
组别 | 学习时间x(h) | 人数(人) |
A | 2.5<x≤3 | 40 |
B | 3<x≤3.5 | 170 |
C | 3.5<x≤4 | 350 |
D | 4<x≤4.5 | |
E | 4.5<x≤5 | 90 |
F | 5小时以上 | 50 |
表1
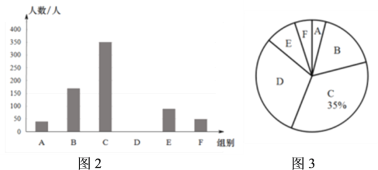
(1)这次参与问卷调查的初中学生有 人,中位数落在 组.
(2)图3中D组对应的角度是 ,并补全图2 条形统计图.
(3)若某市有初中学生2.8万人,请估计每天参与“空中课堂”学习时间3.5到4.5小时(不包括3.5小时)的初中学生有多少人?