��Ŀ����
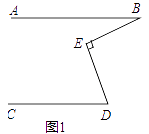
����Ŀ����ͼ1������ABC�У���BAC=90����AB=AC��BDƽ����ABC��
��1���ӳ�BA��M��ʹAM=AD������CM������ACM�Ķ�����
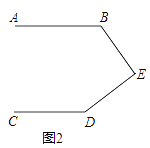
��2����ͼ2����CE��BD��E����BD��EC����������������ϵ����˵������.
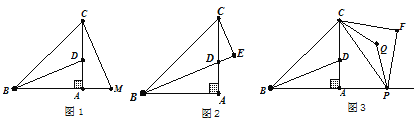
��3����ͼ3����P������BA��A���ұ�һ���㣬��CPΪб��������ֱ����CPF��������F=90������QΪ��FCP����CPF�Ľ�ƽ���ߵĽ��㣮����P�˶�ʱ����Q�Ƿ�һ��������BD�ϣ����ڣ���֤��������������˵�����ɣ�
���𰸡���1��22.5�㣻��2��BD=2CE�����ɼ���������3����Qһ��������BD��.
���������������: ��1��ͨ��֤����BDA�ա�MCA,�õ���DBA=��MCA,�ٸ���BDƽ�֡�ABC�á�ABD��22.5�����õ���ACM��22.5�㣻
(2)�ӳ�CE��BA���ӳ����ڵ�G��ͨ���ж���ABD�ա�ACG���ó�BD��CG��2CE���ɣ�
(3)����CQ������Q��QM��BP��M����QN��BC��N���ڵ���ֱ����CPF�У���á�QCP����QPC��22.5���������ó���PQC�У���PQC��135�������ı���QNBM�У�����QM��BP��QN��BC����ABC��45�����õ���MQN��135���������õ���NQC����MQP������AAS�ж���QPM�ա�QCN���ó�QM��QN�������ݽ�ƽ���ߵ����ʶ������涨�����ó���Qһ��������BD�ϣ�
�������:
��1���ߡ�BAC��90����
���CAM=90��,
���BAC����CAM��
�֡�AB��AC��AM=AD��
���BDA�ա�MCA,
���DBA=��MCA,
��BDƽ�֡�ABC,
���ABD��22.5����
���ACM ��22.5����
�ʴ�Ϊ��22.5����
��2����ͼ���ӳ�CE��BA���ӳ����ڵ�G��
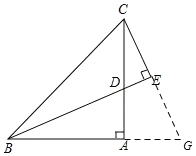
��BDƽ�֡�ABC��CE��BD��
��CE��GE��
�ڡ�ABD���ACG�У�
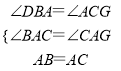 ��
��
���ABD�ա�ACG��AAS����
��BD��CG��2CE��
��3����Qһ��������BD�ϣ�
���ɣ���ͼ������CQ������Q��QM��BP��M����QN��BC��N��
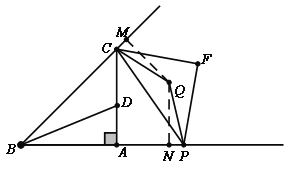
��QFΪ��PFC�Ľ�ƽ���ߣ���CPFΪ����ֱ�������Σ�
��QFΪPC�Ĵ�ֱƽ���ߣ�
��PQ��QC��
��QΪ��FPC���PFC�Ľ�ƽ���ߵĽ��㣬
��CQƽ�֡�FCP��
�ߡ�CPFΪ����ֱ�������Σ�
���FCP����FPC��45����
���QCP����QPC��22.5����
���PQC����PQC��135����
�����ı���QNBM�У�QM��BP��QN��BC����ABC��45����
���MQN��135����
���MQN����PQC��
���NQC����MQP��
�֡�QC��QP��QM��BP��QN��BC��
���QPM�ա�QCN��AAS����
��QM��QN��
�֡�QM��BP��QN��BC��
���Qһ��������BD�ϣ�
�㾦: ������Ҫ�����������ε��ۺ�Ӧ�ã�����ʱ��Ҫ�����������ڽǺͶ���������ֱ�������ε����ʡ���ƽ���ߵĶ����Լ�ȫ�������ε��ж������ʵ�֪ʶ���������Ĺؼ����������ߣ�����ȫ�������Σ�����ȫ�������ε����ʽ����Ƶ�������ʱע�⣺�������߾�����ȵĵ�������ǵ�ƽ�����ϣ�

 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�