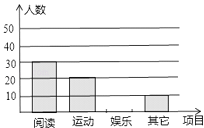
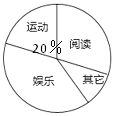
题目内容
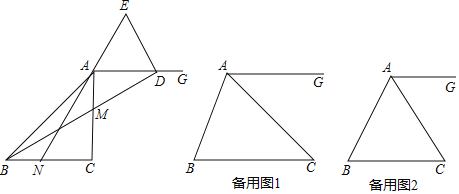
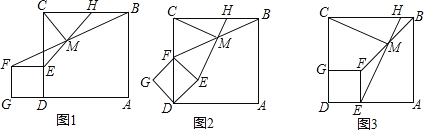
【题目】如图1,点E是正方形ABCD边CD上任意一点,以DE为边作正方形DEFG,连接BF,点M是线段BF中点,射线EM与BC交于点H,连接CM.
(1)请直接写出CM和EM的数量关系和位置关系;
(2)把图1中的正方形DEFG绕点D顺时针旋转45°,此时点F恰好落在线段CD上,如图2,其他条件不变,(1)中的结论是否成立,请说明理由;
(3)把图1中的正方形DEFG绕点D顺时针旋转90°,此时点E、G恰好分别落在线段AD、CD上,如图3,其他条件不变,(1)中的结论是否成立,请说明理由.
【答案】(1)CM=EM,CM⊥EM,理由见解析;(2)(1)中的结论成立,理由见解析;(3)(1)中的结论成立,理由见解析.
【解析】(1)延长EM交AD于H,证明△FME≌△AMH,得到HM=EM,根据等腰直角三角形的性质可得结论;
(2)根据正方形的性质得到点A、E、C在同一条直线上,根据直角三角形斜边上的中线是斜边的一半证明即可;
(3)根据题意画出完整的图形,根据平行线分线段成比例定理、等腰三角形的性质证明即可.
(1)如图1,结论:CM=EM,CM⊥EM.
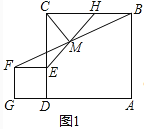
理由:∵AD∥EF,AD∥BC,
∴BC∥EF,
∴∠EFM=∠HBM,
在△FME和△BMH中,
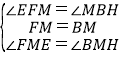 ,,
,,
∴△FME≌△BMH,
∴HM=EM,EF=BH,
∵CD=BC,
∴CE=CH,∵∠HCE=90°,HM=EM,
∴CM=ME,CM⊥EM.
(2)如图2,连接AE,
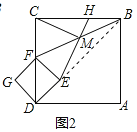
∵四边形ABCD和四边形EDGF是正方形,
∴∠FDE=45°,∠CBD=45°,
∴点B、E、D在同一条直线上,
∵∠BCF=90°,∠BEF=90°,M为AF的中点,
∴CM=![]() AF,EM=
AF,EM=![]() AF,
AF,
∴CM=ME,
∵∠EFD=45°,
∴∠EFC=135°,
∵CM=FM=ME,
∴∠MCF=∠MFC,∠MFE=∠MEF,
∴∠MCF+∠MEF=135°,
∴∠CME=360°-135°-135°=90°,
∴CM⊥ME.
(3)如图3,连接CF,MG,作MN⊥CD于N,
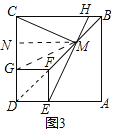
在△EDM和△GDM中,
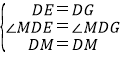 ,
,
∴△EDM≌△GDM,
∴ME=MG,∠MED=∠MGD,
∵M为BF的中点,FG∥MN∥BC,
∴GN=NC,又MN⊥CD,
∴MC=MG,
∴MD=ME,∠MCG=∠MGC,
∵∠MGC+∠MGD=180°,
∴∠MCG+∠MED=180°,
∴∠CME+∠CDE=180°,
∵∠CDE=90°,
∴∠CME=90°,
∴(1)中的结论成立.