题目内容
【题目】如图,在平面直角坐标系中,点A在第一象限,点P在x轴上,若以P,O,A为顶点的三角形是等腰三角形,则满足条件的点P共有个. 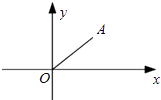
【答案】4或2
【解析】解:以O为圆心,以OA为半径画弧交x轴于点P和P′,此时三角形是等腰三角形,即2个; 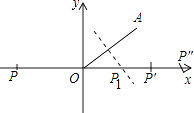
以A为圆心,以OA为半径画弧交x轴于点P″(O除外),此时三角形是等腰三角形,即1个;
作OA的垂直平分线交x轴于一点P1 ,
则AP=OP,
此时三角形是等腰三角形,即1个;
2+1+1=4,
当OA与x轴正半轴夹角等于60°的时候,图中的P1,P'和P'会重合,是一个点,加上原来的负半轴的P点,总共2个点,
所以答案是4或2.
【考点精析】解答此题的关键在于理解等腰三角形的判定的相关知识,掌握如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等.

练习册系列答案
相关题目