题目内容
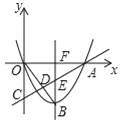
【题目】抛物线y=ax2﹣2x与x轴正半轴相交于点A，顶点为B．
（1）用含a的式子表示点B的坐标；
（2）经过点C（0，﹣2）的直线AC与OB（O为原点）相交于点D，与抛物线的对称轴相交于点E，△OCD≌△BED，求a的值．
【答案】（1）（
，﹣）；（2）
．
【解析】
试题分析：（1）利用配方法即可求得B的坐标；
（2）依据△OCD≌△BED可得BE=CO，据此即可求得BF的长，根据B的坐标求得a的值．
试题解析：（1）y=ax2﹣2x=
，则B的坐标是（，﹣）；
（2）∵点C的坐标是（0，﹣2），∴OC=2，设抛物线的对称轴与x轴相交于点F．
∵EF∥y轴，F是OA的中点，∴EF=
CO=1．
∵△OCD≌△BED，∴BE=CO=2，∴BF=BE+EF=3，∴﹣=﹣3，∴a=．
练习册系列答案
相关题目
