题目内容
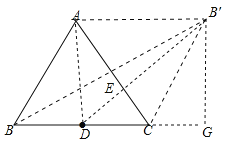
【题目】如图,在边长为2的等边△ABC中,D为BC的中点,E是AC边上一点,则BE+DE的最小值为 .

【答案】![]() .
.
【解析】
试题分析:作B关于AC的对称点B′,连接BB′、B′D,交AC于E,此时BE+ED=B′E+ED=B′D,根据两点之间线段最短可知B′D就是BE+ED的最小值,∵B、B′关于AC的对称,∴AC、BB′互相垂直平分,∴四边形ABCB′是平行四边形,∵三角形ABC是边长为2,∵D为BC的中点,∴AD⊥BC,∴AD=![]() ,BD=CD=1,BB′=2AD=
,BD=CD=1,BB′=2AD=![]() ,作B′G⊥BC的延长线于G,∴B′G=AD=
,作B′G⊥BC的延长线于G,∴B′G=AD=![]() ,
,
在Rt△B′BG中,BG=![]() =
=![]() =3,∴DG=BG﹣BD=3﹣1=2,
=3,∴DG=BG﹣BD=3﹣1=2,
在Rt△B′DG中,BD=![]() =
=![]() =
=![]() .故BE+ED的最小值为
.故BE+ED的最小值为![]() .
.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目