Question

【题目】对于平面直角坐标系xOy中的点P和⊙M，给出如下定义：若⊙M上存在两个点A，B，使AB=2PM，则称点P为⊙M的“美好点”.

(1)当⊙M半径为2，点M和点O重合时，

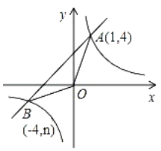
①点P1(-2，0)，P2(1，1)，P3(2，2)中，⊙O的“美好点”是______；

②点P为直线y=x+b上一动点，点P为⊙O的“美好点”，求b的取值范围；

(2)点M为直线y=x上一动点，以2为半径作⊙M，点P为直线y=4上一动点，点P为⊙M的“美好点”，求点M的横坐标m的取值范围.

Answer 1

【答案】(1)①P1，P2；②；(2)2≤m≤6.

【解析】

利用圆的性质，圆的切线定理可依次推导出.

解：(1)①因为

则有当AB最长为直径时，“美好点”在圆周上；

当AB小于直径时，2PM＜直径，“美好点”在圆内.

所以点P的轨迹在圆内部和圆周上.

P1(-2，0)在圆上，P2（1,1）在圆内； P3（2,2）在圆外，所以选P1和P2.

②当直线与⊙O相切时，直线与X轴正向夹角为45°.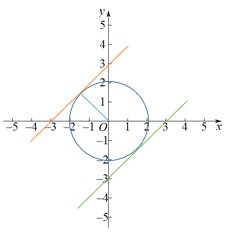

如图：直线与圆相切，则有或；

∴.

(2) 因为点M为直线上一动点, 点P作为⊙M的“美好点”又是直线上一动点,

直线 可以得到直线与X轴正向夹角为45°.

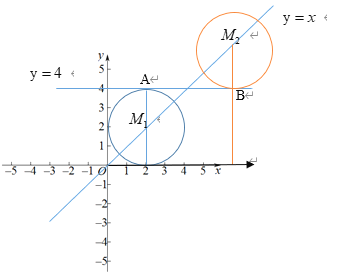
⊙M半径为2,考虑临界情况: ⊙M与相切

∴当直线y=4与⊙M相切时，则有

M1在 下方，此时M1横坐标即为2

M2在 上方, M2的横坐标为2+4=6.

∴ .