题目内容
【题目】(7分)如图,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]()
![]() 在第一象限
在第一象限
的图象交于![]() 点,过
点,过![]() 点作
点作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,已知
,已知![]() 的面积为1.
的面积为1.
(1)求反比例函数的解析式;
(2)如果![]() 为反比例函数在第一象限图象上的点(点
为反比例函数在第一象限图象上的点(点![]() 与点
与点![]() 不重合),且
不重合),且![]() 点的横坐标为1,在
点的横坐标为1,在![]() 轴上求一点
轴上求一点![]() ,使
,使![]() 最小.
最小.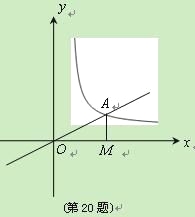
【答案】解:(1)设![]() 点的坐标为(
点的坐标为(![]() ,
,![]() ),则
),则![]() .∴
.∴![]() .
.
∵![]() ,∴
,∴![]() .∴
.∴![]() .
.
∴反比例函数的解析式为![]() .··································································· 3分
.··································································· 3分
(2) 由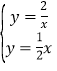 得
得![]() ∴
∴![]() 为(
为(![]() ,
,![]() ). ·············································· 4分
). ·············································· 4分
设![]() 点关于
点关于![]() 轴的对称点为
轴的对称点为![]() ,则
,则![]() 点的坐标为(
点的坐标为(![]() ,
,![]() ).
).
令直线![]() 的解析式为
的解析式为![]() .
.
∵![]() 为(
为(![]() ,
,![]() )∴
)∴![]() ∴
∴![]()
∴![]() 的解析式为
的解析式为![]() .···································································· 6分
.···································································· 6分
当![]() 时,
时,![]() .∴
.∴![]() 点为(
点为(![]() ,
,![]() ). ······················································ 7分
). ······················································ 7分
【解析】
试题(1)设出A点的坐标,然后根据△OAM的面积为1,确定出k的值即可;(2)分别求出点A、B的坐标以及点A关于![]() 轴的对称点C的坐标,然后求出直线BC的解析式,直线BC与x轴的交点即为所求.
轴的对称点C的坐标,然后求出直线BC的解析式,直线BC与x轴的交点即为所求.
试题解析:(1)设A点的坐标为(![]() ,
,![]() ),
),
则![]() .∴
.∴![]() .
.
∵![]() ,∴
,∴![]() .∴
.∴![]() .
.
∴反比例函数的解析式为![]() .
.
(2) 由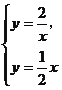 得
得![]() 或
或![]() ∴A为
∴A为![]() .
.
设A点关于![]() 轴的对称点为C,则C点的坐标为
轴的对称点为C,则C点的坐标为![]() .
.
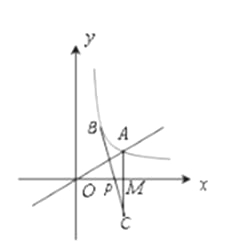
如要在![]() 轴上求一点P,使PA+PB最小.则P点应为BC和x轴的交点,如图所示.
轴上求一点P,使PA+PB最小.则P点应为BC和x轴的交点,如图所示.
令直线BC的解析式为![]() .
.
∵B为(![]() ,
,![]() ),∴
),∴![]() ∴
∴![]()
∴BC的解析式为![]() .
.
当![]() 时,
时,![]() .∴P点坐标为
.∴P点坐标为 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目