题目内容
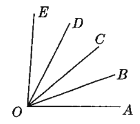
【题目】如图,直线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() ,
,![]() .
.
(1)若![]() ,请求出
,请求出![]() 的度数;
的度数;
(2)![]() 平分
平分![]() 吗?为什么?
吗?为什么?
【答案】(1)155°;(2)OP平分∠EOF,理由见解析
【解析】
(1)根据对顶角相等、角平分线的性质求得∠BOP![]() ∠AOD=25°;然后由邻补角的定义推知∠DOP=180°﹣∠COP;
∠AOD=25°;然后由邻补角的定义推知∠DOP=180°﹣∠COP;
(2)根据垂直的定义、角平分线的定义求得∠EOP=∠FOP.
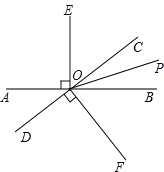
(1)∵直线AB与CD相交于点O,∴∠BOC=∠AOD=50°.
∵OP是∠BOC的平分线,∴∠COP=![]() ∠BOC=
∠BOC=![]() ×50°=25°,∴∠DOP=∠COD-∠COP=180°-25°=155°;
×50°=25°,∴∠DOP=∠COD-∠COP=180°-25°=155°;
(2)OP平分∠EOF.理由如下:
∵OE⊥AB,OF⊥CD,∴∠EOB=∠COF=90°.
∵OP是∠BOC的平分线,∴∠POC=∠POB,∴∠EOB-∠POB=∠COF-∠POC,即∠EOP=∠FOP,∴OP平分∠EOF.

练习册系列答案
相关题目