题目内容
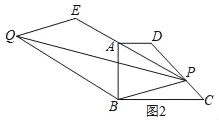
【题目】如图,在Rt△ABC中,∠ACB=90,AD平分∠BAC,过A,C,D三点的圆与斜边AB交于点E,连接DE. 
(1)求证:AC=AE;
(2)若AC=6,CB=8,求△ACD的外接圆的直径.
【答案】
(1)证明:∵AD平分∠BAC,
∴∠CAD=∠EAD,
∴ ![]() =
= ![]() ,
,
∴CD=ED
∵∠ACD=90°,
∴AD是⊙O的直径,
∴ ![]() =
= ![]() ,
,
∴AC=AE
(2)在Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴AB= ![]() =10,
=10,
BE=10﹣AE=10﹣6=4,
设CD=DE=x,
BD=8﹣x,
在Rt△BDE中.BD2=DE2+BE2
(8﹣x)2+x2=42
x=3,即BD=3,
在Rt△ACD中,AD= ![]() =3
=3 ![]()
【解析】(1)根据角平分线的性质、圆周角、弧、弦之间的关系得到 ![]() =
= ![]() ,证明结论;(2)根据勾股定理求出AB,设CD=DE=x,根据勾股定理列出方程,求出x,计算即可.
,证明结论;(2)根据勾股定理求出AB,设CD=DE=x,根据勾股定理列出方程,求出x,计算即可.
【考点精析】认真审题,首先需要了解三角形的外接圆与外心(过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心).

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目