题目内容
【题目】已知四边形ABCD，AD∥BC，AB⊥BC，AD=1，AB=2，BC=3．
（1）如图1，若P为AB边上一点以PD，PC为边作平行四边形PCQD，请问对角线PQ的长是否存在最小值？如果存在，请求出最小值，如果不存在，请说明理由．
（2）若P为AB边上任意一点，延长PD到E，使DE=PD，再以PE，PC为边作平行四边形PCQE，请问对角线PQ的长是否也存在最小值？如果存在，请直接写出最小值，如果不存在，请说明理由．
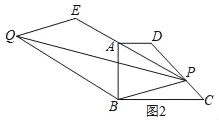
（3）如图2，若P为直线DC上任意一点，延长PA到E，使AE=AP，以PE、PB为边作平行四边形PBQE，请问对角线PQ的长是否存在最小值？如果存在，请求出最小值，如果不存在，请说明理由．
【答案】（1）存在，理由见解析，当PQ⊥AB时，PQ的长最小，即为4．
（2）存在，理由见解析， 当PQ⊥AB时，PQ的长最小，即为5．
（3）存在，理由见解析，最小值为
【解析】试题分析：（1）在平行四边形PCQD中，设对角线PQ与DC相交于点G，则G是DC的中点，过点Q作QH⊥BC，交BC的延长线于H，使得Rt△ADP≌Rt△HCQ，进而求出最小值；
（2）设PQ与DC相交于点G，作QH⊥BC，交BC的延长线于H，可得Rt△ADP∽Rt△HCQ，进而求出最小值；
（3）设PQ与AB相交于点G，由平行线分线段成比例定理可得
.作QH∥PD，交CB的延长线于H，过点C作CK⊥CD，交QH的延长线于K，可证△ADP∽△BHQ，
从而
.过点D作DM⊥BC于M，则四边形ABND是矩形，可求∠DCM=45°，从而求出CD、CK的值，可知当D与P重合时的PQ长就是PQ的最小值.
解：（1）存在，理由如下：
如图2，在平行四边形PCQD中，设对角线PQ与DC相交于点G，
则G是DC的中点，
过点Q作QH⊥BC，交BC的延长线于H，
∵AD∥BC，AB⊥BC，
∴AD⊥AB，∠ADC=∠DCH，
即∠ADP+∠PDG=∠DCQ+∠QCH，
∵PD∥CQ，
∴∠PDC=∠DCQ，
∴∠ADP=∠QCH，
在△ADP和△HCQ中，
，
∴△ADP≌△HCQ（AAS），
∴AD=HC，
∵AD=1，BC=3，
∴BH=4，
∴当PQ⊥AB时，PQ的长最小，即为4．
（2）存在，理由如下：
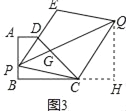
如图3，设PQ与DC相交于点G，
∵四边形PCQE是平行四边形，
∴PE∥CQ，PE=CQ，
∴
，
∵PD=DE，
∴CQ=2PD，
∴
=
,
∴G是DC上一定点，
作QH⊥BC，交BC的延长线于H，
同（2）得：∠ADP=∠QCH，
∴Rt△ADP∽Rt△HCQ，
∴
=，
∴CH=2，
∴BH=BC+CH=3+2=5，
∴当PQ⊥AB时，PQ的长最小，即为5．
（3）存在，理由如下：
如图4，设PQ与AB相交于点G，
∵四边形PBQE是平行四边形，
∴PE∥BQ，PE=BQ，
∴
，
∵AE=PA，
∴BQ=2PA，
∴
=
作QH∥PD，交CB的延长线于H，过点C作CK⊥CD，交QH的延长线于K，
∵AD∥BC，AB⊥BC，
∴∠ADP=∠QHC，∠DAP+∠PAG=∠QBH+∠QBG=90°，∠PAG=∠QBG，
∴∠QBH=∠PAD，
∴△ADP∽△BHQ，
∴
=，
∵AD=1，
∴BH=2，
∴CH=BH+BC=2+3=5，
过点D作DM⊥BC于M，
则四边形ABND是矩形，
∴BM=AD=1，DM=AB=2
∴CM=BC﹣BM=3﹣1=2=DM，
∴∠DCM=45°，
∴∠KCH=45°，
∴CK=CHcos45°=5×
=
，
在Rt△CDM中，CD=2
，
∴CK＞CD，
∴当PQ⊥CD时，PQ的长最小，但是，P点已经不在CD上了，到延长线上了，
∴当D与P重合时的PQ长就是PQ的最小值，
此时Q与H重合，PQ=HD=
=
=
∴最小值为
