题目内容
【题目】如图所示的二次函数y=ax2+bx+c的图象中,刘星同学观察得出了下面四条信息:
①b2﹣4ac>0;②c>1;③2a﹣b<0;④a+b+c<0.你认为其中错误的有( )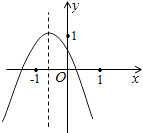
A.2个
B.3个
C.4个
D.1个
【答案】D
【解析】解:①根据图示知,该函数图象与x轴有两个交点,
∴△=b2﹣4ac>0;
故本选项正确;
②由图象知,该函数图象与y轴的交点在点(0,1)以下,
∴c<1;
故本选项错误;
③由图示,知
对称轴x=﹣ ![]() >﹣1;
>﹣1;
又函数图象的开口方向向下,
∴a<0,
∴﹣b<﹣2a,即2a﹣b<0,
故本选项正确;
④根据图示可知,当x=1,即y=a+b+c<0,
∴a+b+c<0;
故本选项正确;
综上所述,我认为其中错误的是②,共有1个;
故选D.
【考点精析】通过灵活运用二次函数图象以及系数a、b、c的关系,掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)即可以解答此题.

练习册系列答案
相关题目
【题目】如图是一个在平面直角坐标系中从原点开始的回形图,其中回形通道的宽和OA的长都是1.
(1)观察图形填写表格:
点 | 坐标 | 所在象限或坐标轴 |
A | ||
B | ||
C | ||
D | ||
E | ||
F |

(2)在图上将回形图继续画下去(至少再画出4个拐点);
(3)说出回形图中位于第一象限的拐点的横坐标与纵坐标之间的关系;
(4)观察图形,说出(3)中的关系在第三象限中是否存在?



