题目内容
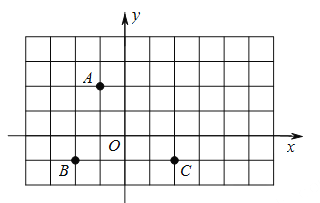
【题目】如图，在平面直角坐标系上有点
，点
第一次跳动至点
，第二次点
跳动至点
，第三次点
跳动至点
，第四次点
跳动至点
，……依此规律跳动下去，则点
与点
之间的距离是（ ）
A. 2021B. 2020C. 2019D. 2018
【答案】A
【解析】
根据图形观察发现，第偶数次跳动至点的坐标，横坐标是次数的一半加上1，纵坐标是次数的一半，奇数次跳动的横坐标是相邻的下次偶数次跳动的横坐标的相反数加上1，纵坐标相同，可分别求出点A2019与点A2020的坐标，进而可求出点A2019与点A2020之间的距离．
观察发现，第2次跳动至点的坐标是（2，1），第4次跳动至点的坐标是（3，2），第6次跳动至点的坐标是（4，3），第8次跳动至点的坐标是（5，4），…
第2n次跳动至点的坐标是（n+1，n），则第2020次跳动至点的坐标是（1011，1010），第2019次跳动至点A2019的坐标是（﹣1010，1010）．
∵点A2019与点A2020的纵坐标相等，∴点A2019与点A2020之间的距离=1011﹣（﹣1010）=2021．
故选A．
练习册系列答案
相关题目
