题目内容
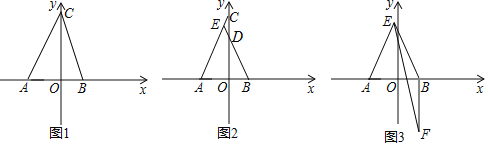
【题目】如图点A(a,0)在x轴负半轴,点B(b,0)在x轴正半轴,点C(0,c)在y轴正半轴,且![]() .
.
(1)如图1,求S△ABC;
(2)如图2,若点D(0,5),BD的延长线交AC于E,求∠AEB;
(3)如图3,在(2)的条件下,将线段BA绕点B逆时针旋转90°至线段BF,连接EF,试探究EA,EB,EF之间有怎样的数量关系,并证明.
【答案】(1)![]() ;(2)45°;(3)
;(2)45°;(3)![]() ,证明详见解析
,证明详见解析
【解析】
(1)根据非负数的性质得到a=﹣3,b=2,c=7,于是得到点A(﹣3,0),点B(2,0),点C(0,7),求得OA=3,OB=2,OC=7,根据三角形的面积公式即可得到结论;
(2)根据勾股定理得到AC=![]() =
=![]() ,过C作CH∥BD交x轴于H,求得直线BD的解析式为:yBD=﹣
,过C作CH∥BD交x轴于H,求得直线BD的解析式为:yBD=﹣![]() x+2,得到直线CH的解析式为yCH=﹣
x+2,得到直线CH的解析式为yCH=﹣![]() x+7,求得H(
x+7,求得H(![]() ,0),得到OH=
,0),得到OH=![]() ,根据勾股定理得到CH=
,根据勾股定理得到CH=![]() =
=![]() ,过A作AM⊥CH于M,根据三角形的面积公式得到AM=
,过A作AM⊥CH于M,根据三角形的面积公式得到AM=![]() ,根据等腰直角三角形的判定和性质得到∠CAM=∠ACM=45°,根据平行线的性质即可得到结论;
,根据等腰直角三角形的判定和性质得到∠CAM=∠ACM=45°,根据平行线的性质即可得到结论;
(3)根据旋转的性质得到△ABF是等腰直角三角形,得到AB=BF,∠ABF=90°,把△EBF绕着点B顺时针旋转90°得到△ABQ,推出△EBQ是等腰直角三角形,根据勾股定理即可得到结论.
解:(1)∵![]() +(b﹣2)2+|c﹣7|=0,
+(b﹣2)2+|c﹣7|=0,
∴a+3=0,b﹣2+0,c﹣7=0,
∴a=﹣3,b=2,c=7,
∴点A(﹣3,0),点B(2,0),点C(0,7),
∴OA=3,OB=2,OC=7,
∴S△ABC=![]() ABOC=
ABOC=![]() ×5×7=
×5×7=![]() ;
;
(2)∵AC=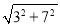 =
=![]() ,
,
∵点D(0,5),
∴BD=![]() ,
,
如图,过C作CH∥BD交x轴于H,
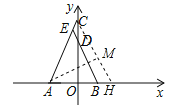
∵点B(2,0),点D(0,5),
∴直线BD的解析式为:yBD=﹣![]() x+2,
x+2,
∴直线CH的解析式为yCH=﹣![]() x+7,
x+7,
当y=0时,x=![]() ,
,
∴H(![]() ,0),
,0),
∴OH=![]() ,
,
∴CH=![]() =
=![]() ,
,
过A作AM⊥CH于M,
∵S△ACH=![]() AHOC=
AHOC=![]() CHAM,
CHAM,
∴AM×![]() =
=![]() ×7,
×7,
∴AM=![]() ,
,
∴CM=![]() =
=![]() ,
,
∴AM=CM,
∴∠CAM=∠ACM=45°,
∵BE∥CH,
∴∠AEB=∠ACH=45°;
(3)∵将线段BA绕点B逆时针旋转90°至线段BF,
∴△ABF是等腰直角三角形,
∴AB=BF,∠ABF=90°,
如图3,把△EBF绕着点B顺时针旋转90°得到△ABQ,
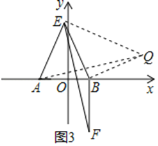
∴△EBQ是等腰直角三角形,
∴∠QEB=45°,EF=AQ,
∴∠AEQ=90°,
∴EF2=AQ2=AE2+EQ2=AE2+2BE2,
故答案为:![]() .
.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案