题目内容
【题目】问题情境
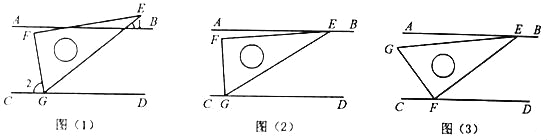
在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含60°角的直角三角尺EFG(∠EFG=90°,∠EGF=60°)”为主题开展数学活动.
操作发现
(1)如图(1),小明把三角尺的60°角的顶点G放在CD上,若∠2=2∠1,求∠1的度数;
(2)如图(2),小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明∠AEF与∠FGC之间的数量关系;
结论应用
(3)如图(3),小亮把三角尺的直角顶点F放在CD上,30°角的顶点E落在AB上.若∠AEG=α,则∠CFG等于______(用含α的式子表示).

【答案】(1)∠1=40°;(2)∠AEF+∠GFC=90°;(3)60°﹣α.
【解析】
(1)依据AB∥CD,可得∠1=∠EGD,再根据∠2=2∠1,∠FGE=60°,即可得出∠EGD![]() (180°﹣60°)=40°,进而得到∠1=40°;
(180°﹣60°)=40°,进而得到∠1=40°;
(2)根据AB∥CD,可得∠AEG+∠CGE=180°,再根据∠FEG+∠EGF=90°,即可得到∠AEF+∠GFC=90°;
(3)根据AB∥CD,可得∠AEF+∠CFE=180°,再根据∠GFE=90°,∠GEF=30°,∠AEG=α,即可得到∠GFC=180°﹣90°﹣30°﹣α=60°﹣α.
(1)如图1.
∵AB∥CD,∴∠1=∠EGD.
又∵∠2=2∠1,∴∠2=2∠EGD.
又∵∠FGE=60°,∴∠EGD![]() (180°﹣60°)=40°,∴∠1=40°;
(180°﹣60°)=40°,∴∠1=40°;
(2)如图2.
∵AB∥CD,∴∠AEG+∠CGE=180°,即∠AEF+∠FEG+∠EGF+∠FGC=180°.
又∵∠FEG+∠EGF=90°,∴∠AEF+∠GFC=90°;
(3)如图3.
∵AB∥CD,∴∠AEF+∠CFE=180°,即∠AEG+∠FEG+∠EFG+∠GFC=180°.
又∵∠GFE=90°,∠GEF=30°,∠AEG=α,∴∠GFC=180°﹣90°﹣30°﹣α=60°﹣α.
故答案为:60°﹣α.

【题目】某出版社出版适合中学生阅读的科普读物,该读物首次出版印刷的印数不少于5000册时,投入的成本与印数间的相应数据如下表:
印数x(册) | 5000 | 8000 | 11000 | 14000 | … |
成本y(元) | 28500 | 36000 | 43500 | 51000 | … |
(1)通过对上表中数据的探究,你发现这种读物的投入成本y(元)是印数x(册)的正比例函数?还是一次函数?并求出这个函数的表达式(不要求写出x的取值范围);
(2)如果出版社投入成本60000元,那么能印该读物多少册?


