Question

【题目】三角形ABC中,AB=5, ,BC边上的高AD=4,BC=__________

Answer 1

【答案】7或1

【解析】

分两种情况讨论：锐角三角形和钝角三角形，根据勾股定理求得BD，CD，再由图形求出BC，在锐角三角形中，BC=BD+CD，在钝角三角形中，BC=CD-BD．

解：（1）如图

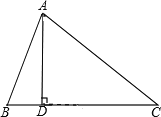
AB=5，，BC边上的高AD=4，
在Rt△ABD中AB=5，AD=4，由勾股定理得
BD2=AB2-AD2，
∴BD=3，
在Rt△ACD中，AD=4，由勾股定理得
CD2=AC2-AD2，
∴CD=3，
∴BC的长为BD+DC=7；
（2）钝角△ABC中，

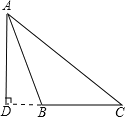
AB=5，，BC边上高AD=4，
在Rt△ABD中AB=5，AD=4，由勾股定理得
BD2=AB2-AD2=132-122=25，
∴BD=4，
在Rt△ACD中，AD=4，由勾股定理得
CD2=AC2-AD2，
∴CD=3，
∴BC的长为DC-BD=1．
故答案为7或1．