题目内容
【题目】如图,抛物线y=ax2+bx+![]() 与直线AB交于点A(﹣1,0),B(4,
与直线AB交于点A(﹣1,0),B(4,![]() ),点D是抛物线A、B两点间部分上的一个动点(不与点A、B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.
),点D是抛物线A、B两点间部分上的一个动点(不与点A、B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.
(1)求抛物线的表达式;
(2)设点D的横坐标为m,△ADB的面积为S,求S关于m的函数关系式,并求出当S取最大值时的点C的坐标.

【答案】(1)y=﹣![]() x2+2x+
x2+2x+![]() (2) C(
(2) C(![]() ,
,![]() )
)
【解析】分析: (1)将点A、B的坐标代入抛物线的解析式,求得a、b的值,从而得到抛物线的解析式;
(2)设直线AB为:y=kx+b.将A、B的坐标代入可得到k,b的方程组,从而可求得k,b于是得到直线AB的解析式,记CD与x轴的交点坐标为E.过点B作BF⊥DC,垂足为F.设D(m,﹣![]() m2+2m+
m2+2m+![]() )则C(m,
)则C(m,![]() m+
m+![]() ),依据三角形的面积公式可得到S与m的函数关系式,接下来由抛物线的对称轴方程,可求得m的值,于是可得到点C的坐标.
),依据三角形的面积公式可得到S与m的函数关系式,接下来由抛物线的对称轴方程,可求得m的值,于是可得到点C的坐标.
详解:
(1)∵由题意得 ,解得:
,解得: ,
,
∴y=﹣![]() x2+2x+
x2+2x+![]() .
.
(2)设直线AB为:y=kx+b.则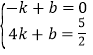 ,解得
,解得![]()
直线AB的解析式为y=![]() +
+![]() .
.
如图所示:记CD与x轴的交点坐标为E.过点B作BF⊥DC,垂足为F.
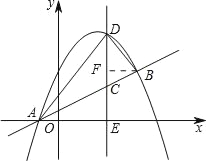
设D(m,﹣![]() m2+2m+
m2+2m+![]() )则C(m,
)则C(m,![]() m+
m+![]() ).
).
∵CD=(﹣![]() m2+2m+
m2+2m+![]() )﹣(
)﹣(![]() m+
m+![]() )=
)=![]() m2+
m2+![]() m+2,
m+2,
∴S=![]() AEDC+
AEDC+![]() CDBF=
CDBF=![]() CD(AE+BF)=
CD(AE+BF)=![]() DC=
DC=![]() m2+
m2+![]() m+5.
m+5.
∴S=![]() m2+
m2+![]() m+5.
m+5.
∵﹣![]() <0,
<0,
∴当m=![]() 时,S有最大值.
时,S有最大值.
∴当m=![]() 时,
时,![]() m+
m+![]() =
=![]() ×
×![]() +
+![]() =
=![]() .
.
∴点C(![]() ,
,![]() ).
).
点睛: 本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求一次函数、二次函数的解析式、三角形的面积公式、二次函数的性质,用含m的式子表示出CD的长,从而得到S与m的关系式是解题的关键.

练习册系列答案
相关题目





