Question

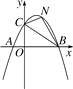
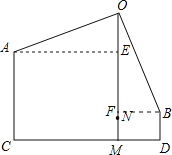
【题目】在一款名为超级玛丽的游戏中，玛丽到达一个高为10米的高台A，利用旗杆顶部的绳索，划过90°到达与高台A水平距离为17米，高为3米的矮台B，求旗杆的高度OM和玛丽在荡绳索过程中离地面的最低点的高度MN．

Answer 1

【答案】2m

【解析】

试题分析：首先得出△AOE≌△OBF（AAS），进而得出CD的长，进而求出OM，MN的长即可．

解：作AE⊥OM，BF⊥OM，

∵∠AOE+∠BOF=∠BOF+∠OBF=90°

∴∠AOE=∠OBF

在△AOE和△OBF中，

，

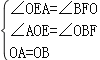∴△AOE≌△OBF（AAS），

∴OE=BF，AE=OF

即OE+OF=AE+BF=CD=17（m）

∵EF=EM﹣FM=AC﹣BD=10﹣3=7（m），

∴2EO+EF=17，

则2×EO=10，

所以OE=5m，OF=12m，

所以OM=OF+FM=15m

又因为由勾股定理得ON=OA=13，

所以MN=15﹣13=2（m）．

答：旗杆的高度OM为15米，玛丽在荡绳索过程中离地面的最低点的高度MN为2米．