题目内容
【题目】如图，直线l1：y1=-
x+m与y轴交于点A(0，6)，直线l2：y2=kx+1分别与x轴交于点B(-2，0)，与y轴交于点C，两条直线l1、l2相交于点D，连接AB．
(1)求两直线l1、l2交点D的坐标；
(2)求△ABD的面积．
【答案】(1)D点坐标为(4，3)；(2)S△ABD=15.
【解析】
(1)将A(0，6)代入y1=-
x+m，即可求出m的值，将B(-2，0)代入y2=kx+1即可求出k的值，得到两函数的解析式，组成方程组解求出D的坐标；
(2)由y2=
x+1可知，C点坐标为(0，1)，分别求出△ABC和△ACD的面积，相加即可．
解：(1)将A(0，6)代入y1=-x+m得，m=6；
将B(-2，0)代入y2=kx+1得，k=，
组成方程组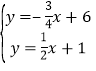得
，解得
，
故D点坐标为(4，3)；
(2)由y2=x+1可知，C点坐标为(0，1)，
S△ABD=S△ABC+S△ACD=×5×2+×5×4=15．
练习册系列答案
名校课堂系列答案
相关题目
【题目】2020年1月以来，由于新型冠状病毒（COVID-19）的肆虐，口罩市场出现热卖，某旗舰网店用8000元购进甲、乙两种口罩，销售完后共获利2800元，进价和售价如右表：
品名 | 甲种口罩 | 乙种口罩 |
进价（元/袋） | 20 | 25 |
售价（元/袋） | 26 | 35 |
（1）求该网店购进甲、乙两种口罩各多少袋？
（2）该网店第二次以原价购进甲、乙、两种口罩，购进乙种口罩袋数不变，而购进甲种口罩袋数是第一次的2倍．甲种口罩按原售价出售，而乙种口罩让利销售．若两种口罩销售完毕，要使第二次销售活动获利不少于3680元，乙种口罩最低售价为每袋多少元？
