题目内容
【题目】如图,直线AB与CD相交于点O,OF,OD分别是∠AOE,∠BOE的平分线.
(1)写出∠DOE的补角;
(2)若∠BOE=62°,求∠AOD和∠EOF的度数;
(3)试问射线OD与OF之间有什么特殊的位置关系?为什么?
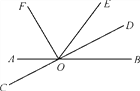
【答案】(1) ∠COE,∠AOD,∠BOC;(2)∠AOD=149°,∠EOF=59°;(3) 射线OD与OF互相垂直,理由见解析.
【解析】试题分析:(1)根据互补的定义确定∠DOE的补角;
(2)先根据角平分线的定义得出∠BOD的度数,再由邻补角定义可得∠AOD=180°-∠BOD;之后根据邻补角定义可得∠AOE=180°-∠BOE,再由角平分线的定义得出∠EOF的度数;
(3)运用平角的定义和角平分线的定义,证明∠DOF是90°,得直线OD、OF的位置关系.
解:(1)∠DOE的补角为:∠COE,∠AOD,∠BOC.
(2)∵OD是∠BOE的平分线,∠BOE=62°,
∴∠BOD=![]() ∠BOE=31°.
∠BOE=31°.
∴∠AOD=180°-∠BOD=149°.
∴∠AOE=180°-∠BOE=118°.
又∵OF是∠AOE的平分线,
∴∠EOF=![]() ∠AOE=59°.
∠AOE=59°.
(3)射线OD与OF互相垂直.理由如下:
∵OF,OD分别是∠AOE,∠BOE的平分线,
∴∠DOF=∠DOE+∠EOF=![]() ∠BOE+
∠BOE+![]() ∠EOA=
∠EOA=![]() (∠BOE+∠EOA)=
(∠BOE+∠EOA)=![]() ×180°=90°.
×180°=90°.
∴OD⊥OF.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目