题目内容
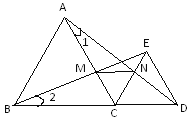
【题目】如图1，直线AB分别与x轴、y轴交于A、B两点，OC平分∠AOB交AB于点C，点D为线段AB上一点，过点D作DE∥OC交y轴于点E，已知AO=m，BO=n，且m、n满足n2﹣12n+36+|n﹣2m|=0．
（1）求A、B两点的坐标；
（2）若点D为AB中点，延长DE交x轴于点F，在ED的延长线上取点G，使DG=DF，连接BG．
①BG与y轴的位置关系怎样？说明理由； ②求OF的长；
（3）如图2，若点F的坐标为（10，10），E是y轴的正半轴上一动点，P是直线AB上一点，且P的横坐标为6，是否存在点E使△EFP为等腰直角三角形？若存在，求出点E的坐标；若不存在，说明理由．
【答案】（1）A（3，0），B（0，6）；（2）①BG与y轴垂直，理由见解析，②OF=1.5（3）存在点E（0，4），使△EFP为等腰直角三角形
【解析】
（1）先求出m，n的值，即可得出结论；
（2）①先判断出△BDG≌△ADF，得出BG=AF，∠G=∠DFA，最后根据平行线的性质得出∠DFA=45°，∠G=45°，即可得出结论；
②利用等腰三角形的性质，建立方程即可得出结论；
（3）先求出点P坐标，进而得出Rt△FME≌Rt△ENP，进而得出求出OE，即可得出结论．
（1）由n2-12n+36+|n-2m|=0．得：（n-6）2+|n-2m|=0，
∴n=6，m=3，
∴A（3，0），B（0，6）．
（2）①BG⊥y轴．
在△BDG与△ADF中，
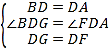
∴△BDG≌△ADF
∴BG=AF，∠G=∠DFA
∵OC平分∠ABC，
∴∠COA=45°，
∵DE∥OC，
∴∠DFA=45°，∠G=45°．
∵∠FOE=90°，
∴∠FEO═45°
∵∠BEG=45°，
∴∠EBG=90°，
即BG与y轴垂直．
②从①可知，BG=FA，△BDE为等腰直角三角形．
∴BG=BE．
设OF=x，则有OE=x，3+x=6-x，解得x=1.5，
即：OF=1.5．
（3）∵A（3，0），B（0，6）．
∵直线AB的解析式为：y=-2x+6，
∵P点的横坐标为6，
故P（6，-6）
要使△EFP为等腰直角三角形，必有EF=EP，且∠FEP═90°，
如图2，过F、P分别向y轴作垂线垂足分别为M、N．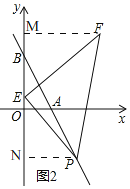
∵∠FEP═90°
∴∠FEM+∠PEN=90°，又∠FEM+∠MFE=90°
∴∠PEN=∠MFE
∴Rt△FME≌Rt△ENP
∴ME=NP=6，
∴OE=10-6=4．
即存在点E（0，4），使△EFP为等腰直角三角形
