题目内容
【题目】如图,已知正方形ABCD中,∠MAN=45°,连接BD与AM,AN分别交于E,F点,则下列结论正确的有_____.
①MN=BM+DN
②△CMN的周长等于正方形ABCD的边长的两倍;
③EF2=BE2+DF2;
④点A到MN的距离等于正方形的边长
⑤△AEN、△AFM都为等腰直角三角形.
⑥S△AMN=2S△AEF
⑦S正方形ABCD:S△AMN=2AB:MN
⑧设AB=a,MN=b,则![]() ≥2
≥2![]() ﹣2.
﹣2.

【答案】①②③④⑤⑥⑦.
【解析】
将△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH.证明△MAN≌△HAN,得到MN=NH,根据三角形周长公式计算判断①;判断出BM=DN时,MN最小,即可判断出⑧;根据全等三角形的性质判断②④;将△ADF绕点A顺时针性质90°得到△ABH,连接HE.证明△EAH≌△EAF,得到∠HBE=90°,根据勾股定理计算判断③;根据等腰直角三角形的判定定理判断⑤;根据等腰直角三角形的性质、三角形的面积公式计算,判断⑥,根据点A到MN的距离等于正方形ABCD的边长、三角形的面积公式计算,判断⑦.
将△ABM绕点A逆时针旋转,使AB与AD重合,得到△ADH.
则∠DAH=∠BAM,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∵∠MAN=45°,
∴∠BAN+∠DAN=45°,
∴∠NAH=45°,
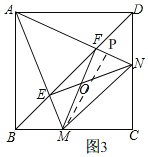
在△MAN和△HAN中,
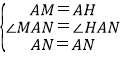 ,
,
∴△MAN≌△HAN,
∴MN=NH=BM+DN,①正确;
∵BM+DN≥2![]() ,(当且仅当BM=DN时,取等号)
,(当且仅当BM=DN时,取等号)
∴BM=DN时,MN最小,
∴BM=![]() b,
b,
∵DH=BM=![]() b,
b,
∴DH=DN,
∵AD⊥HN,
∴∠DAH=![]() ∠HAN=22.5°,
∠HAN=22.5°,
在DA上取一点G,使DG=DH=![]() b,
b,
∴∠DGH=45°,HG=![]() DH=
DH=![]() b,
b,
∵∠DGH=45°,∠DAH=22.5°,
∴∠AHG=∠HAD,
∴AG=HG=![]() b,
b,
∴AB=AD=AG+DG=![]() b+
b+![]() b=
b=![]() b=a,
b=a,
∴![]() ,
,
∴![]() ,
,
当点M和点B重合时,点N和点C重合,此时,MN最大=AB,
即:![]() ,
,
∴![]() ≤
≤![]() ≤1,⑧错误;
≤1,⑧错误;
∵MN=NH=BM+DN
∴△CMN的周长=CM+CN+MN=CM+BM+CN+DN=CB+CD,
∴△CMN的周长等于正方形ABCD的边长的两倍,②结论正确;
∵△MAN≌△HAN,
∴点A到MN的距离等于正方形ABCD的边长AD,④结论正确;
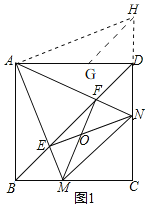
如图2,将△ADF绕点A顺时针性质90°得到△ABH,连接HE.
∵∠DAF+∠BAE=90°-∠EAF=45°,∠DAF=∠BAE,
∴∠EAH=∠EAF=45°,
∵EA=EA,AH=AD,
∴△EAH≌△EAF,
∴EF=HE,
∵∠ABH=∠ADF=45°=∠ABD,
∴∠HBE=90°,
在Rt△BHE中,HE2=BH2+BE2,
∵BH=DF,EF=HE,
∵EF2=BE2+DF2,③结论正确;
∵四边形ABCD是正方形,
∴∠ADC=90°,∠BDC=∠ADB=45°,
∵∠MAN=45°,
∴∠EAN=∠EDN,
∴A、E、N、D四点共圆,
∴∠ADN+∠AEN=180°,
∴∠AEN=90°
∴△AEN是等腰直角三角形,
同理△AFM是等腰直角三角形;⑤结论正确;
∵△AEN是等腰直角三角形,同理△AFM是等腰直角三角形,
∴AM=![]() AF,AN=
AF,AN=![]() AE,
AE,
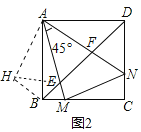
如图3,过点M作MP⊥AN于P,
在Rt△APM中,∠MAN=45°,
∴MP=AMsin45°,
∵S△AMN=![]() ANMP=
ANMP=![]() AMANsin45°,
AMANsin45°,
S△AEF=![]() AEAFsin45°,
AEAFsin45°,
∴S△AMN:S△AEF=2,
∴S△AMN=2S△AEF,⑥正确;
∵点A到MN的距离等于正方形ABCD的边长,
∴S正方形ABCD:S△AMN=![]() =2AB:MN,⑦结论正确.
=2AB:MN,⑦结论正确.
即:正确的有①②③④⑤⑥⑦,
故答案为①②③④⑤⑥⑦.

【题目】已知抛物线y=(x-1)2-1.
(1)该抛物线的对称轴是______________,顶点坐标为____________;
(2)选取适当的数据填入下表,并在图中的直角坐标系内描点画出该抛物线;
x | … | … | |||||
y | … | … |

(3)根据图象,直接写出当y<0时,x的取值范围.






