题目内容
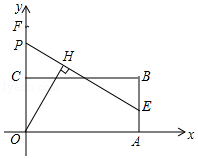
【题目】如图1，过等边三角形ABC边AB上一点D作DE∥BC交边AC于点E，分别取BC，DE的中点M，N，连接MN．
（1）发现：在图1中， 
=；
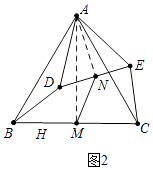
（2）应用：如图2，将△ADE绕点A旋转，请求出 的值；
（3）拓展：如图3，△ABC和△ADE是等腰三角形，且∠BAC=∠DAE，M，N分别是底边BC，DE的中点，若BD⊥CE，请直接写出 的值．
【答案】
（1）
（2）
解：如图2中，连接AM、AN．
∵△ABC，△ADE都是等边三角形，BM=MC，DN=NE，
∴AM⊥BC，AN⊥DE，
∴ 
=sin60°， 
=sin60°，
∴ = ，
∵∠MAB=∠DAN=30°，
∴∠BAD=∠MAN，
∴△BAD∽△MAN，
∴ 
= =sin60°=
（3）
解：如图3中，连接AM、AN，延长AD交CE于H，交AC于O．
∵AB=AC，AD=AE，BM=CM，DN=NE，
∴AM⊥BC，AN⊥DE，
∵∠BAC=∠DAE，
∴∠ABC=∠ADE，
∴sin∠ABM=sin∠ADN，
∴ = ，
∵∠BAM= 
BAC，∠DAN= ∠DAE，
∴∠BAM=∠DAN，
∴∠BAD=∠MAN．
∴△BAD∽△MAN，
∴ = =sin∠ABC，
∵∠BAC=∠DAE，
∴∠BAD=∠CAE，
∵AB=AC，AD=AE，
∴△BAD≌△CAE，
∴∠ABD=∠ACE，
∵BD⊥CE，
∴∠BHC=90°，
∴∠ACE+∠COH=90°，∵∠AOB=∠COH，
∴∠ABD+∠AOB=90°，
∴∠BAO=90°，
∵AB=AC，
∴∠ABC=45°，
∴ 
=sin45°= 
【解析】解：（1）如图1中，作DH⊥BC于H，连接AM．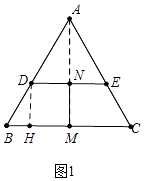
∵AB=AC，BM=CM，
∴AM⊥BC，
∵△ADE时等边三角形，
∴∠ADE=60°=∠B，
∴DE∥BC，
∵AM⊥BC，
∴AM⊥DE，
∴AM平分线段DE，
∵DN=NE，
∴A、N、M共线，
∴∠NMH=∠MND=∠DHM=90°，
∴四边形MNDH时矩形，
∴MN=DH，
∴ = 
=sin60°= ，
所以答案是 ．
【考点精析】解答此题的关键在于理解相似三角形的性质的相关知识，掌握对应角相等，对应边成比例的两个三角形叫做相似三角形．
