ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯп![]() гыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌЕуPДгЕуAГіЗЂЃЌбиелЯпABЉBOЯђжеЕуOдЫЖЏЃЌдкABЩЯвдУПУы5ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌдкBOЩЯвдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏ;ЕуQДгЕуOГіЗЂЃЌбиOAЗНЯђвдУПУы
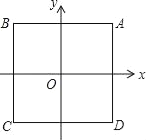
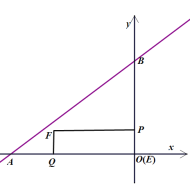
гыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌЕуPДгЕуAГіЗЂЃЌбиелЯпABЉBOЯђжеЕуOдЫЖЏЃЌдкABЩЯвдУПУы5ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏЃЌдкBOЩЯвдУПУы3ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏ;ЕуQДгЕуOГіЗЂЃЌбиOAЗНЯђвдУПУы![]() ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏ.PЃЌQСНЕуЭЌЪБГіЗЂЃЌЕБЕуPЭЃжЙЪБЃЌЕуQвВЫцжЎЭЃжЙ.Й§ЕуPзїPEЁЭAOгкЕуEЃЌвдPEЃЌEQЮЊСкБпзїОиаЮPEQFЃЌЩшОиаЮPEQFгыЁїABOжиЕўВПЗжЭМаЮЕФУцЛ§ЮЊS,ЕуPдЫЖЏЕФЪБМфЮЊtУы.
ИіЕЅЮЛГЄЖШЕФЫйЖШдЫЖЏ.PЃЌQСНЕуЭЌЪБГіЗЂЃЌЕБЕуPЭЃжЙЪБЃЌЕуQвВЫцжЎЭЃжЙ.Й§ЕуPзїPEЁЭAOгкЕуEЃЌвдPEЃЌEQЮЊСкБпзїОиаЮPEQFЃЌЩшОиаЮPEQFгыЁїABOжиЕўВПЗжЭМаЮЕФУцЛ§ЮЊS,ЕуPдЫЖЏЕФЪБМфЮЊtУы.
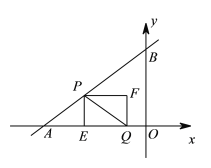
(1)СЌНсPQЃЌЕБPQгыЁїABOЕФвЛБпЦНааЪБЃЌЧѓtЕФжЕ;
(2)ЧѓSгыtжЎМфЕФКЏЪ§ЙиЯЕЪН,ВЂжБНгаДГіздБфСПtЕФШЁжЕЗЖЮЇ.
ЁОД№АИЁПЃЈ1ЃЉЕБ![]() гы
гы![]() ЕФвЛБпЦНааЪБЃЌ
ЕФвЛБпЦНааЪБЃЌ![]() Лђ
Лђ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉ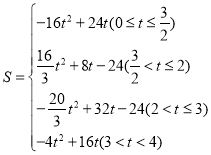
ЁОНтЮіЁП
ЃЈ1ЃЉЯШИљОнвЛДЮКЏЪ§![]() ШЗЖЈЕу
ШЗЖЈЕу![]() ЁЂ
ЁЂ![]() ЕФзјБъЃЌдйгЩ
ЕФзјБъЃЌдйгЩ![]() ЁЂ
ЁЂ![]() ЃЌПЩЕУ
ЃЌПЩЕУ![]() ЁЂ
ЁЂ![]() ЃЌгЩДЫЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЛ
ЃЌгЩДЫЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉИљОнЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЁЂЕу
ЩЯЁЂЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЕФЮЛжУВЛЭЌЁЂздБфСП
ЩЯЕФЮЛжУВЛЭЌЁЂздБфСП![]() ЕФЗЖЮЇВЛЭЌЃЌНјааЗжРрЬжТлЃЌЕУГі
ЕФЗЖЮЇВЛЭЌЃЌНјааЗжРрЬжТлЃЌЕУГі![]() гы
гы![]() ЕФЗжЖЮКЏЪ§ЃЎ
ЕФЗжЖЮКЏЪ§ЃЎ
НтЃКЃЈ1ЃЉЁпдк![]() жаЃЌСю
жаЃЌСю![]() ЃЌдђ
ЃЌдђ![]() ЃЛСю
ЃЛСю![]() ЃЌдђ
ЃЌдђ![]()
Ёр![]() ЃЌ
ЃЌ![]()
Ёр![]() ЃЌ
ЃЌ![]()
ЂйЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌдђ
ЃЌдђ![]()
Ёр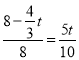
Ёр![]()
ЂкЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌдђ
ЃЌдђ![]()
Ёр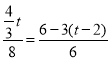
Ёр![]()
ЁрзлЩЯЫљЪіЃЌЕБ![]() гы
гы![]() ЕФвЛБпЦНааЪБЃЌ
ЕФвЛБпЦНааЪБЃЌ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
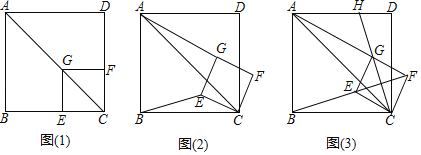
ЃЈ2ЃЉЂйЕБ0ЁмtЁм![]() ЪБЃЌжиЕўВПЗжЪЧОиаЮPEQFЃЌШчЭМЃК
ЪБЃЌжиЕўВПЗжЪЧОиаЮPEQFЃЌШчЭМЃК
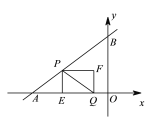
Ёр![]()
Ёр![]()
Ёр![]()
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
Ёр![]() ЃЛ
ЃЛ
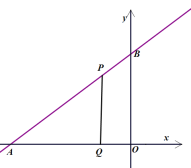
ЂкЕБ![]() ЃМtЁм2ЪБЃЌШчЭМЃЌжиЕўВПЗжЪЧЫФБпаЮPEQMЃЌ
ЃМtЁм2ЪБЃЌШчЭМЃЌжиЕўВПЗжЪЧЫФБпаЮPEQMЃЌ
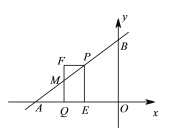
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
взЕУ![]()
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
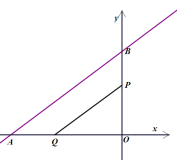
ЂлЕБ2ЃМtЁм3ЪБЃЌжиЕўВПЗжЪЧЮхБпаЮMNPOQЃЌШчЭМЃК
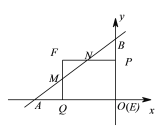
Ёр![]()
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЛ
ЃЛ
ЂмЕБ3ЃМtЃМ4ЪБЃЌжиЕўВПЗжЪЧОиаЮPOQFЃЌШчЭМЃК
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрзлЩЯЫљЪіЃЌ 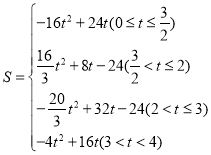 ЃЎ
ЃЎ