题目内容
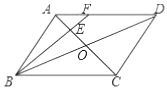
【题目】如图，□ABCD的对角线AC，BD相交于点O，E是以A为圆心，以2为半径的圆上一 动点，连结CE，点P为CE的中点，连结BP，若AC=
，BD=
，则BP的最大值为（ ）
A.
B.
C.
D.
【答案】B
【解析】
连接OP，根据平行四边形对角线互相平分知AO＝CO＝
AC＝a、BO＝DO＝BD＝b，由点P为CE中点得知随着点E的运点，点P的运动轨迹是以O为圆心、1为半径的圆，据此解答可得．
如图，连接OP，
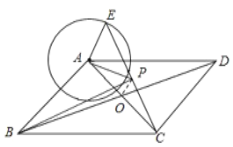
∵四边形ABCD是平行四边形，
∴AO＝CO＝AC＝a，BO＝DO＝BD＝b，
∵点P为CE中点，
∴OP∥AE，且OP＝AE＝1，
∴随着点E的运点，点P的运动轨迹是以O为圆心、1为半径的圆，
则当⊙O与OD交于点P时，BP最大，为BO＋OP＝
，
故选：B．
练习册系列答案
作业辅导系列答案
相关题目
【题目】某企业生产的一种果汁饮料由A、B两种水果配制而成，其比例与成本如下方表格所示，已知该饮料的成本价为8元/千克，按现价售出后可获利润50%，每个月可出售27500瓶．
每千克饮料所占比例 | 成本（元/千克） | |
A | 20% | m |
B | 80% | m-15 |
（1）求m的值；
（2）由于物价上涨，A水果成本提高了25%，B水果成本提高了20%，在不改变售价的情况下，若要保持每个月的利润不减少，则现在至少需要售出多少瓶饮料？
