ΧβΡΩΡΎ»ί
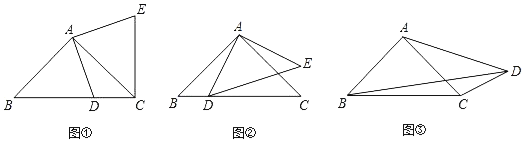
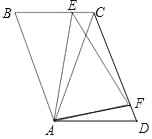
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎRtΓςABC÷–Θ§ΓœACB=90Θ§AB=10Θ§AC=6Θ§ΒψEΓΔFΖ÷±π «±ΏACΓΔBC…œΒΡΕ·ΒψΘ§ΙΐΒψEΉςEDΓΆAB”ΎΒψDΘ§ΙΐΒψFΉςFGΓΆAB”ΎΒψGΘ§DGΒΡ≥Λ Φ÷’ΈΣ2Θ°
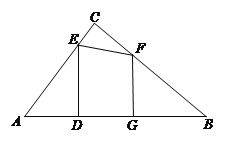
Θ®1Θ©Β±AD=3 ±Θ§«σDEΒΡ≥ΛΘΜ
Θ®2Θ©Β±ΒψEΓΔF‘Ύ±ΏACΓΔBC…œ“ΤΕ· ±Θ§…η![]() Θ§«σyΙΊ”ΎxΒΡΚ· ΐΫβΈω ΫΘ§≤Δ–¥≥ωΚ· ΐΒΡΕ®“ε”ρΘΜ
Θ§«σyΙΊ”ΎxΒΡΚ· ΐΫβΈω ΫΘ§≤Δ–¥≥ωΚ· ΐΒΡΕ®“ε”ρΘΜ
Θ®3Θ© ‘ΎΒψEΓΔF“ΤΕ·Ιΐ≥Χ÷–Θ§ΓςAED”κΓςCEFΡήΖώœύΥΤΘ§»τΡήΘ§«σADΒΡ≥ΛΘΜ»τ≤ΜΡήΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©DE=4ΘΜΘ®2Θ©![]() ΘΜΘ®3Θ©Β±ADΒΡ≥ΛΈΣ
ΘΜΘ®3Θ©Β±ADΒΡ≥ΛΈΣ![]() Μρ
Μρ![]() ±Θ§ΓςAED”κΓςCEFœύΥΤ.
±Θ§ΓςAED”κΓςCEFœύΥΤ.
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΙ¥Ι…Ε®άμœ»«σ≥ωBCΒΡ≥ΛΘ§‘ΌΆ®Ιΐ÷ΛΟςΓςADEΓΉΓςACBΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ΒΟ≥ωDEΒΡ≥ΛΘΜ
Θ®2Θ©Ά®Ιΐ÷ΛΟςΓςBGFΓΉΓςBCAΘ§ΗυΨίœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ΒΟ≥ωyΙΊ”ΎxΒΡΚ· ΐΫβΈω ΫΘΜ
Θ®3Θ©”…Θ®1Θ©Θ®2Θ©Ω…ΒΟΘΚ![]() Θ§Ζ÷ΓœA=ΓœCEFΘ§ΓœA=ΓœCFEΝΫ÷÷«ιΩω«σ≥ωΓςAED”κΓςCEFœύΥΤ ±ADΒΡ≥ΛΘ°
Θ§Ζ÷ΓœA=ΓœCEFΘ§ΓœA=ΓœCFEΝΫ÷÷«ιΩω«σ≥ωΓςAED”κΓςCEFœύΥΤ ±ADΒΡ≥ΛΘ°
ΫβΘΚΘ®1Θ©ΓΏΓœACB=90ΓψΘ§AB=10Θ§AC=6
ΓύBC=8Θ®1Ζ÷Θ©
ΓΏEDΓΆABΓύΓœADE=ΓœACB=90Γψ
”÷ΓΏΓœA=ΓœA
ΓύΓςADEΓΉΓςACB
![]()
ΓύDE=4ΘΜ
Θ®2Θ©ΓΏFGΓΆABΓύΓœBGF=ΓœBCA=90Γψ
”÷ΓΏΓœB=ΓœB
ΓύΓςBGFΓΉΓςBCA
![]()
![]()
![]() ΘΜ
ΘΜ
Θ®3Θ©”…Θ®1Θ©Θ®2Θ©Ω…ΒΟΘΚ![]()
![]()
Β±ΓœA=ΓœCEF ±Θ§![]() ΫβΒΟΘΚ
ΫβΒΟΘΚ![]()
Β±ΓœA=ΓœCFE ±Θ§![]() ΫβΒΟΘΚ
ΫβΒΟΘΚ![]()
ΓύΒ±ADΒΡ≥ΛΈΣ![]() Μρ
Μρ![]() ±Θ§ΓςAED”κΓςCEFœύΥΤΘ°
±Θ§ΓςAED”κΓςCEFœύΥΤΘ°

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
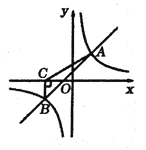
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΡ≥ΑύΓΑ ΐ―ß–Υ»Λ–ΓΉιΓ±Ε‘Κ· ΐy=x2©¹2|x|ΒΡΆΦœσΚΆ–‘÷ Ϋχ––ΝΥΧΫΨΩΘ§ΧΫΨΩΙΐ≥Χ»γœ¬Θ§«κ≤Ι≥δΆξ’ϊΘ°Θ®1Θ©Ή‘±δΝΩxΒΡ»Γ÷ΒΖΕΈß «»ΪΧε Β ΐΘ§x”κyΒΡΦΗΉιΕ‘”Π÷ΒΝ–±μ»γœ¬ΘΚ
x | Γ≠ | ©¹3 | ©¹ | ©¹2 | ©¹1 | 0 | 1 | 2 |
| 3 | Γ≠ |
y | Γ≠ | 3 |
| m | ©¹1 | 0 | ©¹1 | 0 |
| 3 | Γ≠ |
Τδ÷–Θ§m=ΓΓΓΓΘ°
Θ®2Θ©ΗυΨί±μ÷– ΐΨίΘ§‘Ύ»γΆΦΥυ ΨΒΡΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–ΟηΒψΘ§≤ΔΜ≠≥ωΝΥΚ· ΐΆΦœσΒΡ“Μ≤ΩΖ÷Θ§«κΜ≠≥ωΗΟΚ· ΐΆΦœσΒΡΝμ“Μ≤ΩΖ÷Θ°
Θ®3Θ©Ιέ≤λΚ· ΐΆΦœσΘ§–¥≥ωΝΫΧθΚ· ΐΒΡ–‘÷ Θ°
Θ®4Θ©Ϋχ“Μ≤ΫΧΫΨΩΚ· ΐΆΦœσΖΔœ÷ΘΚ
ΔΌΚ· ΐΆΦœσ”κx÷α”–ΓΓΓΓΗωΫΜΒψΘ§Υυ“‘Ε‘”ΠΒΡΖΫ≥Χx2©¹2|x|=0”–ΓΓ ΓΓΗω Β ΐΗυΘΜ
ΔΎΖΫ≥Χx2©¹2|x|=2”–ΓΓΓΓΗω Β ΐΗυ.

ΔέΙΊ”ΎxΒΡΖΫ≥Χx2©¹2|x|=a”–4Ηω Β ΐΗυ ±Θ§aΒΡ»Γ÷ΒΖΕΈß «ΓΓ Θ°