题目内容
【题目】抛物线y=ax2+c与x轴交于A、B两点,顶点为C,点P在抛物线上,且位于x轴下方.
(1)若P(1,﹣3)、B(4,0),
①求该抛物线的解析式;
②若D是抛物线上一点,满足∠DPO=∠POB,求点D的坐标;
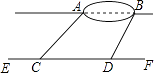
(2)如图2,在(1)中的抛物线解析式不变的条件下,已知直线PA、PB与y轴分别交于E、F两点,点点P运动时,OE+OF是否为定值?若是,试求出该定值;若不是,请说明理由.
【答案】
(1)
解:①将P(1,﹣3),B(4,0)代入y=ax2+c,得 ![]() ,解得
,解得  ,
,
∴抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() ;
;
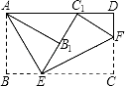
②如图1,

当点D在OP左侧时,
由∠DPO=∠POB,得DP∥OB,
∴D与P关于y轴对称,且P(1,﹣3),
∴D(﹣1,﹣3);
当点D在OP右侧时,延长PD交x轴于点G.
作PH⊥OB于点H,则OH=1,PH=3.
∵∠DPO=∠POB,
∴PG=OG.
设OG=x,则PG=x,HG=x﹣1.
在Rt△PGH中,由x2=(x﹣1)2+32,得x=5.
∴点G(5,0).
∴直线PG的解析式为y= ![]() x﹣
x﹣ ![]() ,
,
解方程组  得
得 ![]() 或
或  ,.
,.
∵P(1,﹣3),
∴D( ![]() ,﹣
,﹣ ![]() ).
).
∴点D的坐标为(﹣1,﹣3)或( ![]() ,﹣
,﹣ ![]() ).
).
(2)
解:点P运动时,OE+OF是定值,定值为2,理由如下:
如图2,作PQ⊥AB于Q点,

设P(m,am2+c),A(﹣t,0),B(t,0),则at2+c=0,c=﹣at2.
∵PQ∥OF,
∴ ![]() =
= ![]() ,
,
∴OF= ![]() =﹣
=﹣ ![]() =
= ![]() ═amt+at2.
═amt+at2.
同理OE=﹣amt+at2,
∴OE+OF=2at2=﹣2c=2OC= ![]() .
.
【解析】(1)①根据待定系数法求函数解析式,可得答案;②根据平行线的判定,可得PD∥OB,根据函数值相等两点关于对称轴对称,可得D点坐标;(2)作PQ⊥AB于Q点,设P(m,am2+c),A(﹣t,0),B(t,0),可表示出OE、OF的长,可得答案.

【题目】为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 25≤x<30 | 4 |
第2组 | 30≤x<35 | 6 |
第3组 | 35≤x<40 | 14 |
第4组 | 40≤x<45 | a |
第5组 | 45≤x<50 | 10 |
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?