题目内容
【题目】乘法公式的探究及应用．
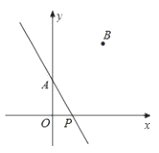
（1）如图 1，可以求出阴影部分的面积是 （写成两数平方差的形式）；
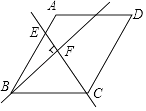
（2）如图 2，若将阴影部分裁剪下来，重新拼成一个矩形，它的宽是 ，长是 ，面积是 （写成多项式乘法的形式）
（3）比较图 1，图 2 的阴影部分面积，可以得到乘法公式 （用式子表达）
（4）应用所得的公式计算：（1﹣
）（1﹣
）（1﹣
）…（1﹣
）（1﹣
）
【答案】（1）a2-b2；（2）a-b，a+b，（a+b）（a-b）；（3）（a+b）（a-b）=a2-b2；（4）
．
【解析】
（1）小题1：利用正方形的面积公式就可求出；
（2）仔细观察图形就会知道长，宽，由面积公式就可求出面积；
（3）建立等式就可得出；
（4）利用平方差公式就可方便计算．
（1）利用正方形的面积公式可知：阴影部分的面积=a2-b2；
故答案为：a2-b2；
（2）由图可知矩形的宽是a-b，长是a+b，所以面积是（a+b）（a-b）；
故答案为：a-b，a+b，（a+b）（a-b）；
（3）（a+b）（a-b）=a2-b2（等式两边交换位置也可）；
故答案为：（a+b）（a-b）=a2-b2；
（4）（1﹣
）（1﹣
）（1﹣
）…（1﹣
）（1﹣
）
=（1-
）（1+）（1-
）（1+）（1-
）（1+）…（1-
）（1+）（1-
）（1+）
=×
=
．
练习册系列答案
阅读快车系列答案
相关题目
【题目】根据实验结果表明，在弹簧的承受范围内，弹簧挂上物体后会伸长，测得一弹簧的长度
与所挂的物体的重量
间有下表的关系，下列说法不正确的是（ ）
| 0 | 1 | 2 | 3 | 4 |
| 20 | 21 | 22 | 23 | 24 |
A.
与
都是变量，且是自变量，是因变量
B.弹簧不挂重物时的长度为
C.随着所挂物体重量的增加，弹簧长度逐渐变长
D.所挂物体的重量每增加
，弹簧长度增加
