题目内容
【题目】在平面直角坐标系中，△OAB三个顶点的坐标分别为O（0，0），A（3，0），B（2，3）．
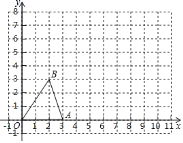
（1）tan∠OAB＝ ；
（2）在第一象限内画出△OA'B'，使△OA'B'与△OAB关于点O位似，相似比为2：1；
（3）在（2）的条件下，S△OAB：S四边形AA′B′B＝ ．
【答案】（1）3；（2）见解析；（3）3
【解析】
（1）根据正切的定义求解可得；
（2）利用位似图形的概念作出点A、B的对应点，再与点O首尾顺次连接即可得；
（3）利用位似变换的性质求解可得．
解：（1）如图，过点B作BC⊥OA于点C，
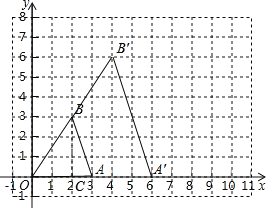
则AC＝1、BC＝3，
∴tan∠OAB＝
＝3，
故答案为：3；
（2）如图所示，△OA'B'即为所求．
（3）∵△OA'B'与△OAB关于点O位似，相似比为2：1，
∴S△OA'B'＝4S△OAB，
则S四边形AA′B′B＝3S△OAB，即S△OAB：S四边形AA′B′B＝1：3，
故答案为：3．
练习册系列答案
相关题目
