Question

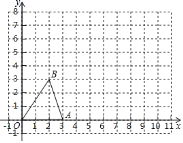
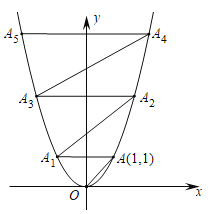
【题目】在平面直角坐标系中， 抛物线如图所示．已知点的坐标为，过点作轴交抛物线于点，过点作交抛物线于点，过点作轴交抛物线于点，过点作交抛物线于点…若依次进行下去，则点的坐标为________．

Answer 1

【答案】

【解析】

根据二次函数性质可得出点A1的坐标，求得直线A1A2为y=x+2，联立方程求得A2的坐标，即可求得A3的坐标，同理求得A4的坐标，即可求得A5的坐标，根据坐标的变化找出变化规律，即可找出点A2019的坐标．

解：∵A点坐标为(1,1)，
∴直线OA为y=x，A1(1,1)，
∵A1A2//OA，
∴直线A1A2为y=x+2，
解得或

∴A2(2,4)，
∴A3(2,4)，
∵A3A4//OA，
∴直线A3A4为y=x+6，
解得或

∴A4(3,9)，
∴A5(3,9)
…，
∴A2019(1010,10102)，即A2019
故答案为.