题目内容
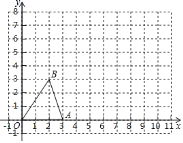
【题目】已知如图所示,在Rt△ABC中,∠A=90°,∠BCA=75°,AC=8cm,DE垂直平分BC,则BE的长是( )

A.4cmB.8cmC.16cmD.32cm
【答案】C
【解析】
连接CE,先由三角形内角和定理求出∠B的度数,再由线段垂直平分线的性质及三角形外角的性质求出∠CEA的度数,由直角三角形中30°所对的直角边是斜边的一半即可解答.
解:连接CE,
∵Rt△ABC中,∠A=90°,∠BCA=75°,
∴∠B=90°﹣∠BCA=90°﹣75°=15°,
∵DE垂直平分BC,
∴BE=CE,
∴∠BCE=∠B=15°,
∴∠AEC=∠BCE+∠B=30°,
∵Rt△AEC中,AC=8cm,
∴CE=2AC=16cm,
∵BE=CE,
∴BE=16cm.
故选:C.

练习册系列答案
相关题目