题目内容
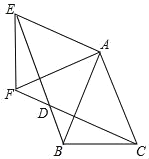
【题目】已知,点P是等边三角形△ABC中一点,线段AP绕点A逆时针旋转60°到AQ,连接PQ、QC.
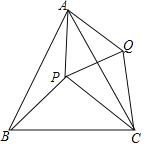
(1)求证:△BAP≌△CAQ.
(2)若PA=3,PB=4,∠APB=150°,求PC的长度.
【答案】(1)见解析;(2)5
【解析】
(1)直接利用旋转的性质结合全等三角形的判定与性质得出答案;
(2)直接利用等边三角形的性质结合勾股定理即可得出答案.
(1)证明:∵线段AP绕点A逆时针旋转60°到AQ,
∴AP=AQ,∠PAQ=60°,
∴△APQ是等边三角形,∠PAC+∠CAQ=60°,
∵△ABC是等边三角形,
∴∠BAP+∠PAC=60°,AB=AC,
∴∠BAP=∠CAQ,
在△BAP和△CAQ中,
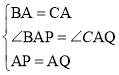 ,
,
∴△BAP≌△CAQ(SAS);
(2)∵由(1)得△APQ是等边三角形,
∴AP=PQ=3,∠AQP=60°,
∵∠APB=150°,
∴∠PQC=150°﹣60°=90°,
∵PB=QC,
∴QC=4,
∴△PQC是直角三角形,
∴PC=![]() =
=![]() =5.
=5.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目