题目内容
已知,二次函数 的图像经过点
的图像经过点 和点B,其中点B在第一象限,且OA=OB,cot∠BAO=2.
和点B,其中点B在第一象限,且OA=OB,cot∠BAO=2.

(1)求点B的坐标;
(2)求二次函数的解析式;
(3)过点B作直线BC平行于x轴,直线BC与二次函数图像的另一个交点为C,联结AC,如果点P在x轴上,且△ABC和△PAB相似,求点P的坐标.
 的图像经过点
的图像经过点 和点B,其中点B在第一象限,且OA=OB,cot∠BAO=2.
和点B,其中点B在第一象限,且OA=OB,cot∠BAO=2.
(1)求点B的坐标;
(2)求二次函数的解析式;
(3)过点B作直线BC平行于x轴,直线BC与二次函数图像的另一个交点为C,联结AC,如果点P在x轴上,且△ABC和△PAB相似,求点P的坐标.
(1)点B的坐标是(3,4),(2)二次函数的解析式是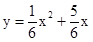
(3)点P的坐标为(6,0)或(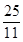 ,0).
,0).
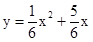
(3)点P的坐标为(6,0)或(
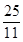 ,0).
,0).试题分析:(1)过点B作BD⊥x轴,垂足为点D,根据余切的定义可设BD=x,AD=2x,在Rt△ODB中根据勾股定理可计算出x,则BD=4,OD=3,所以点B的坐标是(3,4);
(2)利用待定系数法可确定二次函数的解析式;
(3)先确定C点的坐标为(-8,4),则BC=11,AB=4
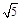 ,由CB∥x轴得到∠ABC=∠BAP,再分类讨论:当△ABC∽△BAP;当△ABC∽△PAB,然后利用比例线段求AP的长,从而确定P点坐标.
,由CB∥x轴得到∠ABC=∠BAP,再分类讨论:当△ABC∽△BAP;当△ABC∽△PAB,然后利用比例线段求AP的长,从而确定P点坐标.试题解析:
解:(1)过点B作BD⊥x轴,垂足为点D
在Rt△ADB中,∠ADB=90º,
cot∠BAO=
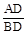 =2.
=2. 设BD=x,AD=2x,由题意,得OA=0B=5,∴OD=2x-5.
在Rt△ODB中,OD2+BD2=OB2,∴
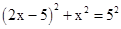 ,
,解得
 ,
,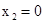 (不合题意,舍去).
(不合题意,舍去).∴BD=4,OD=3,∴点B的坐标是(3,4).
(2)由题意,得
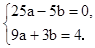 ,解这个方程组,得
,解这个方程组,得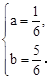
∴二次函数的解析式是
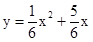
(3)∵直线BC平行于x轴,∴C点的纵坐标为4,设C点的坐标为(m,4).
由题意,得
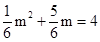 , 解得
, 解得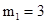 (不合题意,舍去),
(不合题意,舍去),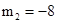 .
.∴C点的坐标为(-8,4), BC=11, AB=
 .
.∵∠ABC=∠BAP,
①如果△ABC∽△BAP,那么
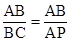 ,
,∴AP=11,点P的坐标为(6,0).m]
②如果△ABC∽△PAB,那么
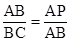 ,
,∴AP=
 ,点P的坐标为(
,点P的坐标为(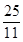 ,0).
,0).综上所述,点P的坐标为(6,0)或(
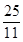 ,0).
,0).
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
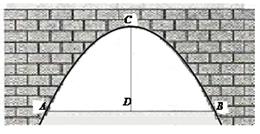
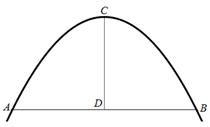
 向右平移
向右平移 个单位,所得新抛物线的函数解析式是( )
个单位,所得新抛物线的函数解析式是( ) ;
; ;
; ;
; .
.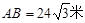 ,
,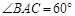 .设
.设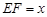 米,
米,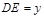 米.
米.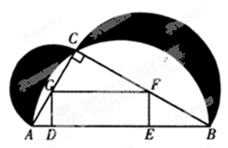
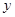 与
与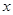 之间的函数解析式;
之间的函数解析式;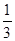 ?
?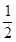 x2
x2 (千克)随销售单价
(千克)随销售单价 (元/千克)的变化而变化,具体关系式为:
(元/千克)的变化而变化,具体关系式为: ,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为
,且物价部门规定这种绿茶的销售单价不得高于90元/千克.设这种绿茶在这段时间内的销售利润为 (元),解答下列问题:
(元),解答下列问题: 厘米,面积随之增加
厘米,面积随之增加 平方厘米,则
平方厘米,则