题目内容
如图①,在□ABCD中,对角线AC⊥AB,BC=10,tan∠B=2.点E是BC边上的动点,过点E作EF⊥BC于点E,交折线AB-AD于点F,以EF为边在其右侧作正方形EFGH,使EH边落在射线BC上.点E从点B出发,以每秒1个单位的速度在BC边上运动,当点E与点C重合时,点E停止运动,设点E的运动时间为t( )秒.
)秒.
(1)□ABCD的面积为 ;当t= 秒时,点F与点A重合;
(2)点E在运动过程中,连接正方形EFGH的对角线EG,得△EHG,设△EHG与△ABC的重叠部分面积为S,请直接写出S与t的函数关系式以及对应的自变量t的取值范围;
(3)作点B关于点A的对称点Bˊ,连接CBˊ交AD边于点M(如图②),当点F在AD边上时,EF与对角线AC交于点N,连接MN得△MNC.是否存在时间t,使△MNC为等腰三角形?若存在,请求出使△MNC为等腰三角形的时间t;若不存在,请说明理由.
 )秒.
)秒.(1)□ABCD的面积为 ;当t= 秒时,点F与点A重合;
(2)点E在运动过程中,连接正方形EFGH的对角线EG,得△EHG,设△EHG与△ABC的重叠部分面积为S,请直接写出S与t的函数关系式以及对应的自变量t的取值范围;
(3)作点B关于点A的对称点Bˊ,连接CBˊ交AD边于点M(如图②),当点F在AD边上时,EF与对角线AC交于点N,连接MN得△MNC.是否存在时间t,使△MNC为等腰三角形?若存在,请求出使△MNC为等腰三角形的时间t;若不存在,请说明理由.

(1)40;2
(2)

(3)
 ,或
,或 ,或
,或
试题分析:
(1)考查学生利用平行四边形和直角三角形解决基本问题的能力,运用直角三角形勾股定理和三角函数即可得解.
(2)关键确定几个分界点,通过题意及动点所在位置,确定几个分界,通过等式得出函数关系式.
(3)注意分类情况,可能是CN="CM" 或MN=MC或 MN=NC,分别解出即可.
试题解析:
(1)∵AC⊥AB,∴在Rt△BAC中BC=10,
tan∠B="2"


又

∴AC=
 ,AB=
,AB= ∴SRt△BAC=40
∴SRt△BAC=40∴BE=2 ∴

(2)依题意得分类可得,①当△EHG与△ABC的重叠部分都
在△ABC内部,S最大面积时,G落在AC上,则
△BEF∽△AFG, AF=
 ,BF=
,BF= ,AF+BF=
,AF+BF= ,∴
,∴ ,S=
,S= (
( )
)②当F点与A点重合时,
 即
即 ,利用相似三角形、线段相互关系和面积关系,得
,利用相似三角形、线段相互关系和面积关系,得S=

③当F点过A点时,则当
 时,利用相似三角形、线段相互关系和面积关系,得
时,利用相似三角形、线段相互关系和面积关系,得S=

④当
 时,利用相似三角形、线段相互关系和面积关系,得
时,利用相似三角形、线段相互关系和面积关系,得S=



(3)CM=CN时,

MC=MN时,

NM=NC时,


练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
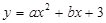 经过
经过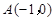 、
、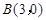 、C三点,点
、C三点,点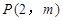 是抛物线与直线
是抛物线与直线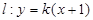 的一个交点.
的一个交点.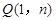 ,求
,求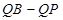 的最大值;
的最大值;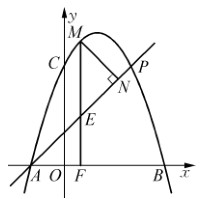
 的一元二次方程
的一元二次方程 .
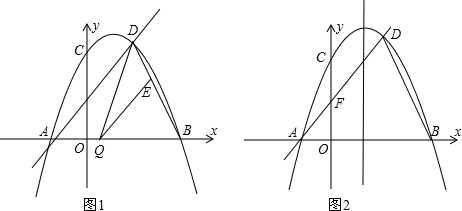
. 与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.点O为坐标原点,点P在直线BC上,且OP=
与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.点O为坐标原点,点P在直线BC上,且OP= BC,求点P的坐标.
BC,求点P的坐标.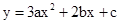 ,
, 求该抛物线与x轴的交点坐标;
求该抛物线与x轴的交点坐标;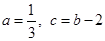 ,证明抛物线与x轴有两个交点;
,证明抛物线与x轴有两个交点;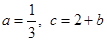 且抛物线在
且抛物线在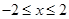 区间上的最小值是-3,求b的值.
区间上的最小值是-3,求b的值.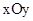 中,抛物线
中,抛物线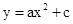 与x轴交于点A(-2,0)和点B,与y轴交于点C(0,
与x轴交于点A(-2,0)和点B,与y轴交于点C(0,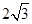 ),线段AC上有一动点P从点A出发,以每秒1个单位长度的速度向点C移动,线段AB上有另一个动点Q从点B出发,以每秒2个单位长度的速度向点A移动,两动点同时出发,设运动时间为t秒.
),线段AC上有一动点P从点A出发,以每秒1个单位长度的速度向点C移动,线段AB上有另一个动点Q从点B出发,以每秒2个单位长度的速度向点A移动,两动点同时出发,设运动时间为t秒.
 DB.
DB.

 上的概率为( )
上的概率为( ) B.
B. C.
C. D.
D.