题目内容
已知抛物线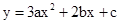 ,
,
(1)若 求该抛物线与x轴的交点坐标;
求该抛物线与x轴的交点坐标;
(2)若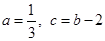 ,证明抛物线与x轴有两个交点;
,证明抛物线与x轴有两个交点;
(3)若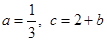 且抛物线在
且抛物线在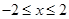 区间上的最小值是-3,求b的值.
区间上的最小值是-3,求b的值.
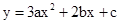 ,
,(1)若
 求该抛物线与x轴的交点坐标;
求该抛物线与x轴的交点坐标;(2)若
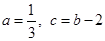 ,证明抛物线与x轴有两个交点;
,证明抛物线与x轴有两个交点;(3)若
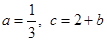 且抛物线在
且抛物线在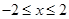 区间上的最小值是-3,求b的值.
区间上的最小值是-3,求b的值.(1)(-1,0)和(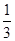 ,0);(2)证明见解析;(3)3或
,0);(2)证明见解析;(3)3或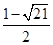 .
.
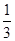 ,0);(2)证明见解析;(3)3或
,0);(2)证明见解析;(3)3或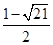 .
.试题分析:(1)将a、b、c的值代入,可得出抛物线解析式,从而可求解抛物线与x轴的交点坐标.
(2)把
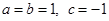 代入抛物线解析式,表示出方程的判别式的表达式,利用配方法及完全平方的非负性即可判断出结论.
代入抛物线解析式,表示出方程的判别式的表达式,利用配方法及完全平方的非负性即可判断出结论.(3)
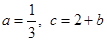 ,则抛物线可化为
,则抛物线可化为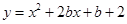 ,其对称轴为x=-b,以-1≤x≤2为区间,讨论b的取值,根据最小值为-3,可得出方程,求出b的值即可.
,其对称轴为x=-b,以-1≤x≤2为区间,讨论b的取值,根据最小值为-3,可得出方程,求出b的值即可.(1)当
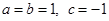 时,抛物线为
时,抛物线为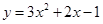 ,
,∵方程
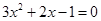 的两个根为x1=-1,x2=
的两个根为x1=-1,x2=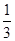 ,
,∴该抛物线与x轴交点的坐标是(-1,0)和(
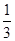 ,0).
,0).(2)当
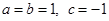 时,抛物线
时,抛物线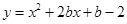 ,
,设y=0,则
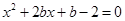 ,
,∴
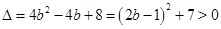 ,
,∴抛物线与x轴有两个交点.
(3)
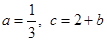 ,则抛物线可化为
,则抛物线可化为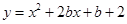 ,其对称轴为x=-b,
,其对称轴为x=-b,当-b<-2时,即b>2,则有抛物线在x=-2时取最小值为-3,
此时-3=(-2)2+2×(-2)b+b+2,
解得:b=3,符合题意.
当-b>2时,即b<-2,则有抛物线在x=2时取最小值为-3,
此时-3=22+2×2b+b+2,
解得:b=
 ,不合题意,舍去.
,不合题意,舍去.当-2≤-b≤2时,即-2≤b≤2,则有抛物线在x=-b时取最小值为-3,
此时-3=(-b)2+2×(-b)b+b+2,
化简得:b2-b-5=0,
解得:b1=
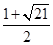 (不合题意,舍去),b2=
(不合题意,舍去),b2=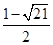 .
.综上可得:b=3或b=
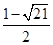 .
.
练习册系列答案
相关题目
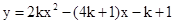 (k是实数).
(k是实数). 时,不是y随x的增大而增大就是y随x的增大而减小;
时,不是y随x的增大而增大就是y随x的增大而减小; )秒.
)秒.
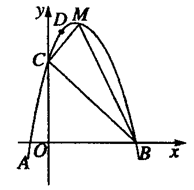
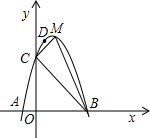
 的图象与
的图象与 轴相交于点
轴相交于点 ,顶点为
,顶点为 ,点
,点 在这个二次函数图象的对称轴上.若四边形
在这个二次函数图象的对称轴上.若四边形 是一个边长为2且有一个内角为
是一个边长为2且有一个内角为 的菱形.求此二次函数的表达式.
的菱形.求此二次函数的表达式.
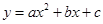 (
(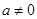 )的图象如图所示,对称轴是直线
)的图象如图所示,对称轴是直线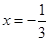 ,有下列结论:①
,有下列结论:①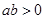 ;②
;②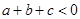 ;③
;③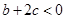 ;④
;④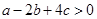 .其中正确结论的个数是( ).
.其中正确结论的个数是( ).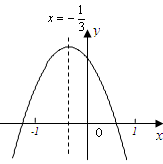
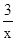 的交点的横坐标x0的取值范围是( )
的交点的横坐标x0的取值范围是( )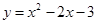 配方后为
配方后为 ,则
,则 .
.