题目内容
已知关于 的一元二次方程
的一元二次方程 .
.
(1)求证:方程总有两个实数根;
(2)若m为整数,当此方程有两个互不相等的负整数根时,求m的值;
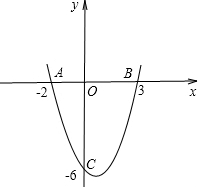
(3)在(2)的条件下,设抛物线 与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.点O为坐标原点,点P在直线BC上,且OP=
与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.点O为坐标原点,点P在直线BC上,且OP= BC,求点P的坐标.
BC,求点P的坐标.
 的一元二次方程
的一元二次方程 .
.(1)求证:方程总有两个实数根;
(2)若m为整数,当此方程有两个互不相等的负整数根时,求m的值;
(3)在(2)的条件下,设抛物线
 与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.点O为坐标原点,点P在直线BC上,且OP=
与x轴交点为A、B(点B在点A的右侧),与y轴交于点C.点O为坐标原点,点P在直线BC上,且OP= BC,求点P的坐标.
BC,求点P的坐标.(1)证明见解析;(2)1;(3)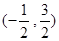 或
或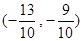 .
.
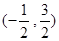 或
或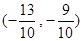 .
.试题分析:(1)证明一元二次方程根的判别式大于等于0即可.
(2)解一元二次方程,根据方程有两个互不相等的负整数根列不等式求解即可.
(3)求出BC的长,由OP=
 BC求得OP;应用待定系数法求出BC 的解析式,从而由点P在直线BC上,设
BC求得OP;应用待定系数法求出BC 的解析式,从而由点P在直线BC上,设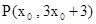 ,应用勾股定理即可求得点P的坐标.
,应用勾股定理即可求得点P的坐标.(1)∵
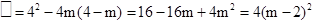 ≥0,
≥0,∴方程总有两个实数根.
(2)∵
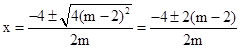 ,
,∴
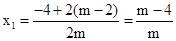 ,
,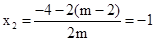 .
.∵方程有两个互不相等的负整数根,
∴
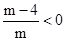 .∴
.∴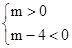 或
或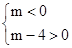 .∴
.∴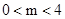 .
.∵m为整数,∴m=1或2或3.
当m=1时,
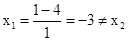 ,符合题意;
,符合题意;当m=2时,
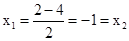 ,不符合题意;
,不符合题意;当m=3时,
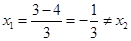 ,但不是整数,不符合题意.
,但不是整数,不符合题意.∴m=1.
(3)m=1时,抛物线解析式为
 .
.令
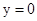 ,得
,得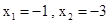 ;令x=0,得y=3.
;令x=0,得y=3.∴A(-3,0),B(-1,0),C(0,3).∴
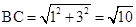 .
.∴OP=
 BC
BC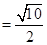 .
.设直线BC的解析式为
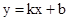 ,
,∴
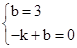 ,∴
,∴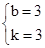 .
.∴直线BC的解析式为
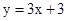 .
.设
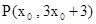 ,由勾股定理有:
,由勾股定理有: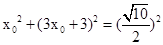 ,
,整理,得
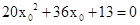 ,解得
,解得 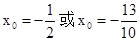 .
.∴
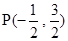 或
或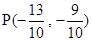 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
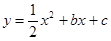 经过A(
经过A( ,0),C(2,-3)两点,与y轴交于点D,与x轴交于另一点B.
,0),C(2,-3)两点,与y轴交于点D,与x轴交于另一点B.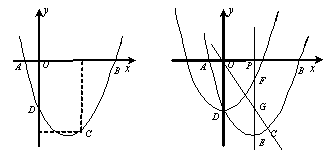
 )秒.
)秒.
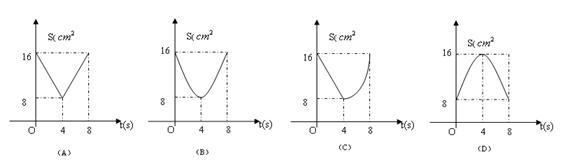
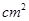 ),则s(
),则s(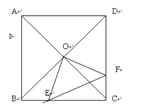
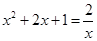 的正数根的个数为( )
的正数根的个数为( ) -1的图像向左平移2个单位,再向上平移1个单位,所得抛物线 .
-1的图像向左平移2个单位,再向上平移1个单位,所得抛物线 .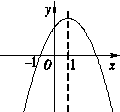

 时,y随x的增大而增大
时,y随x的增大而增大
 是一元二次方程
是一元二次方程 的一个根
的一个根