题目内容
平面直角坐标第xoy中,A点的坐标为(0,5).B、C分别是x轴、y轴上的两个动点,C从A出发,沿y轴负半轴方向以1个单位/秒的速度向点O运动,点B从O出发,沿x轴正半轴方向以1个单位/秒的速度运动.设运动时间为t秒,点D是线段OB上一点,且BD=OC.点E是第一象限内一点,且AE DB.
DB.
(1)当t=4秒时,求过E、D、B三点的抛物线解析式.
(2)当0<t<5时,(如图甲),∠ECB的大小是否随着C、B的变化而变化?如果不变,求出它的大小.
(3)求证:∠APC=45°
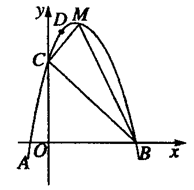
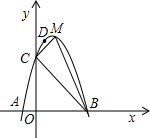
(4)当t>5时,(如图乙)∠APC的大小还是45°吗?请说明理由.


 DB.
DB.(1)当t=4秒时,求过E、D、B三点的抛物线解析式.
(2)当0<t<5时,(如图甲),∠ECB的大小是否随着C、B的变化而变化?如果不变,求出它的大小.
(3)求证:∠APC=45°
(4)当t>5时,(如图乙)∠APC的大小还是45°吗?请说明理由.


(1)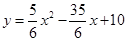 ;(2)∠ECB的大小不变.90°;(3)证明见解析;(4)∠APC>45°.
;(2)∠ECB的大小不变.90°;(3)证明见解析;(4)∠APC>45°.
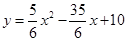 ;(2)∠ECB的大小不变.90°;(3)证明见解析;(4)∠APC>45°.
;(2)∠ECB的大小不变.90°;(3)证明见解析;(4)∠APC>45°.试题分析:(1)当t=4时,知AC=OB=4,进而知OC=1,由BD=OC,AE∥DB,AE=BD可求AE=DB=OC=1,点E、点D、点B的坐标即可确定。再设出抛物线的解析式y=ax2+bx+c,将三点坐标代入即可求出a、b、c的值;
(2)连接CE,可证∠ECB=90°;
(3)由(2)可知:△ECB是等腰直角三角形,继而可证四边形ADBE是平行四边形,从而∠APC=∠EBC=45°;
(4)如图,在第二象限取点F,作AF∥BD,AF=BD,连接CF、BF.易得Rt△ACF≌Rt△OBC,再证△BCF是等腰直角三角形,由三角形的一个外角大于与它不相邻的内角知∠APC>45°.
(1)当t=4秒时,AC=OB=4,由A(0,5)得C(0,1),即OC=1.
又BD=OC,AE DB,
∴AE=DB=OC=1.
∴E(1,5)B(4,0),D(3,0).
设过E、D、B三点的抛物线解析式为y="ax2+bx+c" ,则有
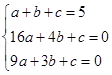 ,解得:
,解得: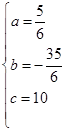 ;
;∴抛物线解析式为
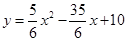 ;
;(2)(2)∠ECB的大小不变。
连接CE。易得Rt△ACE≌Rt△OBC(SAS)
∴CE=CB,∠ACE=∠OBC,∠AEC=∠OCB.
又∠ACE+∠AEC=90°,
∴∠ACE+∠OCB=90°
,∴∠ECB=90°.
(3)由(2)知,CE=CB,∠ECB=90°,
∴△ECB是等腰直角三角形.
∴∠EBC=45°,
又AE
 DB,
DB,∴四边形ADBE是平行四边形.
∴AB∥EB.
∴∠APC=∠EBC=45°.
(4)当t>5时,∠APC>45°,理由如下:
如图,在第二象限取点F,作AF
 BD,连接CF、BF.
BD,连接CF、BF.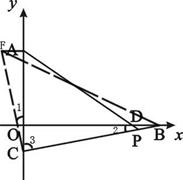
易得Rt△ACF≌Rt△OBC(SAS)
∴CF=CB,∠1=∠2.
又∠1+∠3=90°。∴∠2+∠3=90°即△BCF是等腰直角三角形.
∴∠CBF=45°,又∠APC>∠CBF,
∴∠APC>45°.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
 )秒.
)秒.

 ,该产品的外地销售量y2(万台)与外地广告费用t(万元)之间的函数关系可用如图所示的抛物线和线段AB来表示,其中点A为抛物线的顶点.
,该产品的外地销售量y2(万台)与外地广告费用t(万元)之间的函数关系可用如图所示的抛物线和线段AB来表示,其中点A为抛物线的顶点.

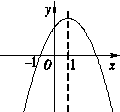

 时,y随x的增大而增大
时,y随x的增大而增大
 是一元二次方程
是一元二次方程 的一个根
的一个根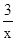 的交点的横坐标x0的取值范围是( )
的交点的横坐标x0的取值范围是( )