Question

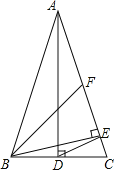
【题目】如图，在△ABC中，AB＝AC═12，AD⊥BC，BE⊥AC，F为AC中点，连接BF、DE，当BE2﹣DE2最大时，则DE长为_______．

Answer 1

【答案】3

【解析】

设CE＝x，则AE＝12﹣x，BE2＝122﹣(12﹣x)2＝24x﹣x2，BC2＝BE2+CE2＝24x，构建二次函数即可解决问题．

解：设CE＝x，则AE＝12﹣x，

∴BE2＝122﹣(12﹣x)2＝24x﹣x2，BC2＝BE2+CE2＝24x，

∵AB＝AC，AD⊥BC，

∴BD＝DC，

∴DEBC，

∴DE2BC2＝6x，

∴BE2﹣DE2＝24x﹣x2﹣6x＝﹣x2+18x＝﹣(x﹣9)2+81，

∵﹣1＜0，

∴x＝9时，BE2﹣DE2的值最大，

∴DE2＝54，

∴DE＝3，

故答案为3．