题目内容
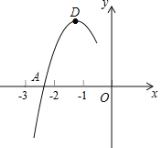
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.
轴交于点A,将点A向右平移2个单位长度,得到点B,点B在抛物线上.
(1)求点B的坐标(用含![]() 的式子表示);
的式子表示);
(2)求抛物线的对称轴;
(3)已知点![]() ,
,![]() .若抛物线与线段PQ恰有一个公共点,结合函数图象,求
.若抛物线与线段PQ恰有一个公共点,结合函数图象,求![]() 的取值范围.
的取值范围.
【答案】(1)点B的坐标为![]() ;(2)对称轴为直线
;(2)对称轴为直线![]() ;(3)当
;(3)当![]() 时,抛物线与线段PQ恰有一个公共点.
时,抛物线与线段PQ恰有一个公共点.
【解析】
(1)![]() 向右平移2个单位长度,得到点
向右平移2个单位长度,得到点![]() ;
;
(2)A与B关于对称轴x=1对称;
(3))①a>0时,当x=2时,![]() ,当
,当![]() 时,x=0或x=2,所以函数与AB无交点;②a<0时,当y=2时,
时,x=0或x=2,所以函数与AB无交点;②a<0时,当y=2时,![]() ,
,![]() 或
或![]() 当
当![]() 时,
时,![]() ;
;
解:(1)∵抛物线与![]() 轴交于点A,∴令
轴交于点A,∴令![]() ,得
,得![]() ,
,
∴点A的坐标为![]() ,∵点A向右平移两个单位长度,得到点B,
,∵点A向右平移两个单位长度,得到点B,
∴点B的坐标为![]() ;
;
(2)∵抛物线过点![]() 和点
和点![]() ,由对称性可得,抛物线对称轴为
,由对称性可得,抛物线对称轴为
直线![]() ,故对称轴为直线
,故对称轴为直线![]()
(3)∵对称轴x=1,
∴b-2a,![]() ,
,
①a>0时,
当x=2时,![]() ,当
,当![]() x=0或x=2,
x=0或x=2,
∴函数与AB无交点;
②a<0时,
当y=2时,![]() ,
,
![]() 或
或![]() 当
当![]() 时,
时,![]() ;
;
∴当![]() 时,抛物线与线段PQ恰有一个公共点;
时,抛物线与线段PQ恰有一个公共点;
(3)①当![]() 时,则
时,则![]() ,分析图象可得:根据抛物线的对称性,抛物线不可能同时经过点A和点P;也不可能同时经过点B和点Q,所以,此时线段PQ与抛物线没有交点.
,分析图象可得:根据抛物线的对称性,抛物线不可能同时经过点A和点P;也不可能同时经过点B和点Q,所以,此时线段PQ与抛物线没有交点.
②当![]() 时,则
时,则![]() .
.
分析图象可得:根据抛物线的对称性,抛物线不可能同时经过点A和点P;但当点Q在点B上方或与点B重合时,抛物线与线段PQ恰有一个公共点,此时![]() 即
即
![]()
综上所述,当![]() 时,抛物线与线段PQ恰有一个公共点.
时,抛物线与线段PQ恰有一个公共点.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
【题目】二次函数![]() =ax2+bx+c的部分对应值如表,利用二次的数的图象可知,当函数值y>0时,x的取值范围是( )
=ax2+bx+c的部分对应值如表,利用二次的数的图象可知,当函数值y>0时,x的取值范围是( )
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 |
y | ﹣12 | ﹣5 | 0 | 3 | 4 | 3 |
A.0<x<2B.x<0或x>2C.﹣1<x<3D.x<﹣1或x>3