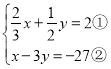题目内容
【题目】已知x1,x2是关于x的方程x2+(3k+1)x+2k2+1=0的两个不相等实数根,且满足(x1﹣1)(x2﹣1)=8k2,则k的值为_____.
【答案】1
【解析】
根据根与系数的关系结合(x1﹣1)(x2﹣1)=8k2,可得出关于k的一元二次方程,解之即可得出k的值,根据方程的系数结合根的判别式△>0,可得出关于k的一元二次不等式,解之即可得出k的取值范围,进而即可确定k值,此题得解.
解:∵x1,x2是关于x的方程x2+(3k+1)x+2k2+1=0的两个实数根,
∴x1+x2=﹣(3k+1),x1x2=2k2+1.
∵(x1﹣1)(x2﹣1)=8k2,即x1x2﹣(x1+x2)+1=8k2,
∴2k2+1+3k+1+1=8k2,
整理,得:2k2﹣k﹣1=0,
解得:k1=﹣![]() ,k2=1.
,k2=1.
∵关于x的方程x2+(3k+1)x+2k2+1=0的两个不相等实数根,
∴△=(3k+1)2﹣4×1×(2k2+1)>0,
解得:k<﹣3﹣2![]() 或k>﹣3+2
或k>﹣3+2![]() ,
,
∴k=1.
故答案为1.

【题目】随着高铁的建设,春运期间动车组发送旅客量越来越大,相关部门为了进一步了解春运期间动车组发送旅客量的变化情况,针对2014年至2018年春运期间的铁路发送旅客量情况进行了调查,过程如下.
(Ⅰ)收集、整理数据
请将表格补充完整:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
动车组发送旅客量a亿人次 | 0.87 | 1.14 | 1.46 | 1.80 | 2.17 |
铁路发送旅客总量b亿人次 | 2.52 | 2.76 | 3.07 | 3.42 | 3.82 |
动车组发送旅客量占比 | 34.5% | 41.3% | 47.6% | 52.6% |
(Ⅱ)描述数据
为了更直观地显示动车组发送旅客量占比的变化趋势,需要用 (填“折线图”或“扇形图”)进行描述;
(Ⅲ)分析数据、做出推测
预估2019年春运期间动车组发送旅客量占比约为 ,你的预估理由是 .