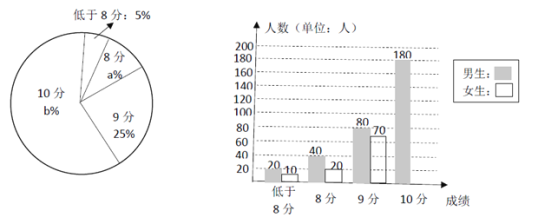
题目内容
【题目】问题提出
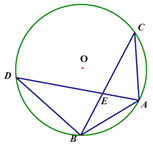
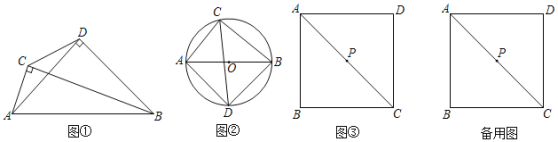
(1)如图1.已知∠ACB=∠ADB=90°,请用尺规作图作出△ABD的外接圆(保留作图痕迹,不写作法);点C是否在△ABD的外接圆上 (填“是”或“否”).
问题探究
(2)如图2.四边形ADBC是⊙O的内接四边形,∠ACB=∠ADB=90°,AD=BD.求证:CA+CB=![]() CD;
CD;
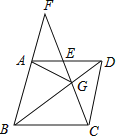
(3)如图3.点P是正方形ABCD对角线AC的中点,点E是平面上一点,EB=AB且EA=![]() BA.点Q是线段AE的中点,请在图中画出点E,并求线段PQ与AB之间的数量关系.
BA.点Q是线段AE的中点,请在图中画出点E,并求线段PQ与AB之间的数量关系.
【答案】问题提出(1)作△ABD的外接圆,见解析;是;问题探究(2)见解析;(3)画出点E,见解析; PQ=![]() AB,PQ=
AB,PQ=![]() AB.
AB.
【解析】
(1)作AB的垂直平分线交AB于点O,以O为圆心,AO长为半径作圆,即为△ABD的外接圆,利用四点共圆的性质可说明C在圆上;
(2)如图2,作辅助线,把AC+BC转化为CE,可证得△CDE是等腰直角三角形,从而右证明结论成立;
(3)以点B为圆心,AB长为半径作圆,以点A为圆心,![]() AB长为半径作圆,两圆的交点为E,注意有两个交点都符合题意;连接BQ,BP,设AB=3x,在Rt
AB长为半径作圆,两圆的交点为E,注意有两个交点都符合题意;连接BQ,BP,设AB=3x,在Rt![]() 中求得
中求得![]() ,易证得AQBP四点共圆且AP=BP,AP⊥BP,运用(2)的结论可求得PQ的值,继而求得线段PQ与AB之间的数量关系.
,易证得AQBP四点共圆且AP=BP,AP⊥BP,运用(2)的结论可求得PQ的值,继而求得线段PQ与AB之间的数量关系.
问题提出
(1)作AB的垂直平分线交AB于点O,以O为圆心,AO长为半径作圆,即为△ABD的外接圆,
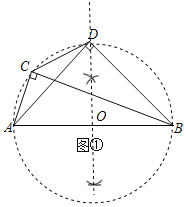
∵∠ACB=∠ADB=90°,
∴点A,点B,点D,点C四点共圆,
∴点C在△ABD的外接圆上,
故答案为:是;
问题探究
(2)如图2,将△BCD绕点D,逆时针旋转90°到△AED处,
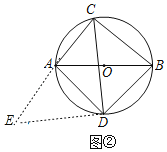
∴∠EAD=∠DBC,
∵四边形ADBC是圆内接四边形,
∴∠DBC+∠DAC=180°,
∴∠EAD+∠DAC=180°,
∴E、A、C三点共线,
∴∠CAE为平角,
由旋转知,AE=BC,DE=CD,∠CDE=90°,
∴△CDE是等腰直角三角形,
∴CE=![]() CD,
CD,
∵CE=AE+AC=BC+AC,
∴CA+CB=![]() CD;
CD;
(3)如图3,连接BQ,BP,
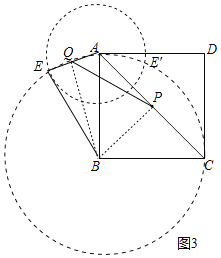
∵以点B为圆心,AB长为半径作圆,以点A为圆心,![]() AB长为半径作圆,两圆的交点为E,
AB长为半径作圆,两圆的交点为E,
∴点A的左右各有个点E,
设AB=3x,则AE=x,
若点E在点A的左侧,
∵BE=AB,点Q是AE的中点,
∴BQ⊥AE,AQ=EQ=![]() ,
,
∴BQ=![]() ,
,
∵四边形ABCD是正方形,点P是对角线AC的中点,
∴AP=BP,AP⊥BP,
由(2)的结论可得:AQ+BQ=![]() PQ,
PQ,
∴![]() PQ=
PQ=![]()
∴PQ=![]() ,
,
∴PQ=![]() ,
,
若点E在点A的右侧,
同理可求:PQ=![]() .
.

 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案