ЬтФПФкШн
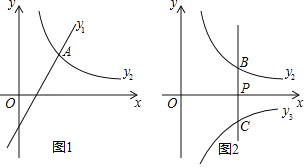
ЁОЬтФПЁПЃЈ1ЃЉШчЭМЂйЃЌдк8ЁС6ЕФЭјИёЭМжаЃЌУПИіаЁе§ЗНаЮБпГЄОљЮЊ1ЃЌдЕуOКЭЁїABCЕФЖЅЕуОљЮЊИёЕуЃЎЕуCзјБъЮЊЃЈ2ЃЌ4ЃЉЃЌвдOЮЊЮЛЫЦжааФЃЌдкЭјИёЭМжазїЁїABCЃЌЪЙЁїAЁфBЁфCЁфгыЁїABCЮЛЫЦЃЌЧвЮЛЫЦБШЮЊ1ЃК2ЃЛЃЈБЃСєзїЭМКлМЃЃЉ
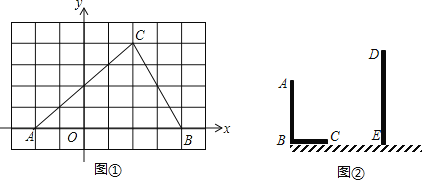
ЃЈ2ЃЉдђЕуCЁфЕФзјБъЮЊЁЁ ЃЌжмГЄБШCЁїAЁфBЁфCЁфЃКCЁїABCЃНЁЁ ЃЎ
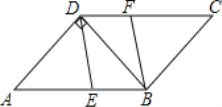
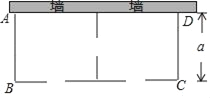
ЃЈ3ЃЉШчЭМЂкЃЌABКЭDEЪЧжБСЂдкЕиУцЩЯЕФСНИљСЂжљЃЎABЃН6mЃЌФГвЛЪБПЬABдкбєЙтЯТЕФЭЖгАBCЃН4mЃЌDEдкбєЙтЯТЕФЭЖгАГЄЮЊ6mЃЎ
ЂйЧыФудкЭМЂкжаЛГіДЫЪБDEдкбєЙтЯТЕФЭЖгАEFЃЎ
ЂкИљОнЬтжааХЯЂЃЌЧѓЕУСЂжљDEЕФГЄЮЊЁЁ mЃЎ
ЁОД№АИЁПЃЈ1ЃЉШчЭМЃЌЁїAЁфBЁфCЁфМДЮЊЫљЧѓзїШ§НЧаЮЃЌМћНтЮіЃЛЃЈ2ЃЉЃЈ1ЃЌ2ЃЉЃЛ1ЃК2ЃЛЃЈ3ЃЉШчЭМЫљЪОЃЌEFОЭЪЧDEЕФЭЖгАЃЎМћНтЮіЃЛЂкDEЃН9mЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУЮЛЫЦЭМаЮЕФаджЪЕУГіAЁфЃЌBЁфЃЌCЁфЕФЮЛжУЃЌНјЖјЕУГіД№АИЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉжаЫљЛЭМаЮПЩЕУЃЛ
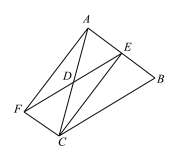
ЃЈ3ЃЉЂйИљОнвбжЊСЌНгACЃЌЙ§ЕуDзїDFЁЮACЃЌМДПЩЕУГіEFОЭЪЧDEЕФЭЖгАЃЛ
ЂкРћгУШ§НЧаЮЁїABCЁзЁїDEFЕУГіБШР§ЪНЃЌЧѓГіDEМДПЩЃЎ
НтЃКЃЈ1ЃЉШчЭМЃЌЁїAЁфBЁфCЁфМДЮЊЫљЧѓзїШ§НЧаЮЃЌ
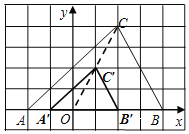
ЃЈ2ЃЉгЩЃЈ1ЃЉжЊЃЌЕуCЁфЕФзјБъЮЊЃЈ1ЃЌ2ЃЉЃЌ
ЁпЮЛЫЦБШЮЊ1ЃК2ЃЌ
ЁржмГЄБШCЁїAЁфBЁфCЁфЃКCЁїABC=1ЃК2ЃЎ
ЙЪД№АИЮЊЃКЃЈ1ЃЌ2ЃЉЃЛ1ЃК2ЃЎ
ЃЈ3ЃЉЂйзїЗЈЃКСЌНгACЃЌЙ§ЕуDзїDFЁЮACЃЌНЛжБЯпBEгкFЃЌ
ШчЭМЫљЪОЃЌЯпЖЮEFОЭЪЧDEЕФЭЖгАЃЎ
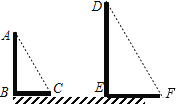
ЂкЁпЬЋбєЙтЯпЪЧЦНааЕФЃЌ
ЁрACЁЮDFЃЎ
ЁрЁЯACBЃНЁЯDFEЃЎ
гжЁпЁЯABCЃНЁЯDEFЃН90ЁуЃЌ
ЁрЁїABCЁзЁїDEFЃЎ
Ёр![]() ЃЌ
ЃЌ
ЁпABЃН6mЃЌBCЃН4mЃЌEFЃН6mЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрDEЃН9mЃЎ
ЙЪД№АИЮЊЃКDEЃН9mЃЎ

 жЧФмбЕСЗСЗВтПМЯЕСаД№АИ
жЧФмбЕСЗСЗВтПМЯЕСаД№АИ МЦЫуИпЪжЯЕСаД№АИ
МЦЫуИпЪжЯЕСаД№АИЁОЬтФПЁПЖўДЮКЏЪ§y=ax2+bx+cЃЈaЃЌbЃЌcЮЊГЃЪ§ЃЌЧвaЁй0ЃЉжаЕФxгыyЕФВПЗжЖдгІжЕШчБэ
x | Љ1 | 0 | 1 | 3 |
y | Љ1 | 3 | 5 | 3 |
ЯТСаНсТлЃК
ЂйacЃМ0ЃЛ
ЂкЕБxЃО1ЪБЃЌyЕФжЕЫцxжЕЕФдіДѓЖјМѕаЁЃЎ
Ђл3ЪЧЗНГЬax2+ЃЈbЉ1ЃЉx+c=0ЕФвЛИіИљЃЛ
ЂмЕБЉ1ЃМxЃМ3ЪБЃЌax2+ЃЈbЉ1ЃЉx+cЃО0ЃЎ
Цфжае§ШЗЕФНсТлЪЧ ЃЎ