Question

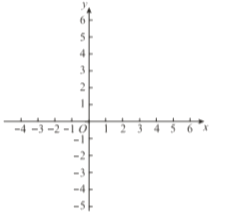
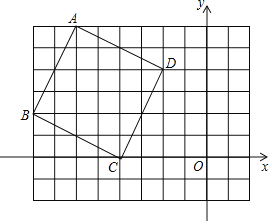
【题目】如图，在平面直角坐标系中，四边形ABCD的坐标分别为A（﹣6，6），B（﹣8，2），C（﹣4，0），D（﹣2，4）．

（1）画出一个四边形A′B′C′D′，使四边形A′B′C′D′与四边形ABCD是以原点O为位似中心，相似比为1：2的位似图形．

（2）直接写出点的坐标：A′（　 　），B′（　 　），C′（　 　），D′（　 　）．

Answer 1

【答案】（1）见解析；（2）（﹣3，3），（﹣4，1），（﹣2，0），（﹣1，2）

【解析】

（1）、（2）把A、B、C、D的横纵坐标都乘以得到四边形A′B′C′D′四个顶点坐标，然后描点即可．

解：（1）如图，四边形A′B′C′D′为所作；

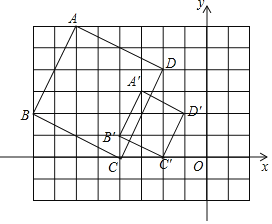
（2）A′（﹣3，3），B′（﹣4，1），C′（﹣2，0），D′（﹣1，2）．

故答案为（﹣3，3），（﹣4，1），（﹣2，0），（﹣1，2）．