题目内容
【题目】(操作发现)
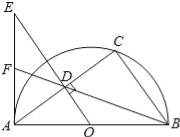
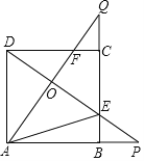
如图①,在正方形ABCD中,点N、M分别在边BC、CD上,连结AM、AN、MN.
∠MAN=45°,将△AMD绕点A顺时针旋转90°,点D与点B重合,得到△ABE.易证:△ANM≌△ANE,从而得DM+BN=MN.
(实践探究)
(1)在图①条件下,若CN=3,CM=4,则正方形ABCD的边长是 .
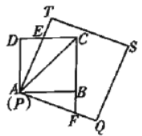
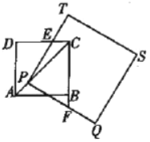
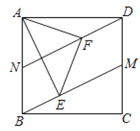
(2)如图②,点M、N分别在边CD、AB上,且BN=DM.点E、F分别在BM、DN上,∠EAF=45°,连接EF,猜想三条线段EF、BE、DF之间满足的数量关系,并说明理由.
(拓展)
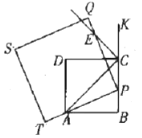
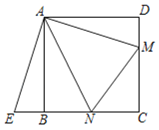
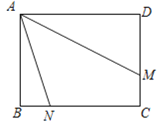
(3)如图③,在矩形ABCD中,AB=3,AD=4,点M、N分别在边DC、BC上,连结AM,AN,已知∠MAN=45°,BN=1,求DM的长.
【答案】(1)6;(2)![]() ,见解析;(3)2
,见解析;(3)2
【解析】
(1)根据旋转的性质证明△ABE≌△ADM得到BE=DM,又由∠ABE=∠D=90°,AE=AM,∠BAE=∠DAM,证出∠EAM=90°,得出∠MAN=∠EAN,再证明△AMN≌△EAN(SAS),得出MN=EN最后证出MN=BN+DM.在Rt△CMN中,由勾股定理计算即可得到正方形的边长;
(2 )先根据旋转的性质证明△AEG≌△AEF(SAS),再证明∠GBE=90°,再根据勾股定理即可得到;
(3)在AB上截取AP,在BC上截取BQ,使AP=AB=BQ=3,连结PQ交AM于点R,得到ABQP为正方形,再根据操作发现以及勾股定理即可得到答案;
(1)(1)解:∵四边形ABCD是正方形,
∴AB=CD=AD,∠BAD=∠C=∠D=90°,
由旋转得:△ABE≌△ADM,
∴BE=DM,∠ABE=∠D=90°,AE=AM,∠BAE=∠DAM,
∴∠BAE+∠BAM=∠DAM+∠BAM=∠BAD=90°,
即∠EAM=90°,
∵∠MAN=45°,
∴∠EAN=90°-45°=45°,
∴∠MAN=∠EAN,
在△AMN和△EAN中,
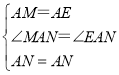
∴△AMN≌△EAN(SAS),
∴MN=EN.
∵EN=BE+BN=DM+BN,
∴MN=BN+DM.
在Rt△CMN中,
![]() ,
,
则BN+DM=5,
设正方形ABCD的边长为x,则BN=BC-CN=x-3,DM=CD-CM=x-4,
∴x-3+x-4=5,
解得:x=6,
即正方形ABCD的边长是6;
故答案为:6;
(2)数量关系为:![]() ,证明如下:
,证明如下:
将△AFD绕点A顺时针旋转90°,点D与点B重合,得到△ABG,连结EG.
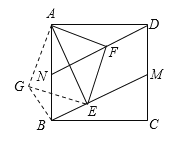
由旋转的性质得到:AF=AG,![]()
又∵∠EAF=45°,
∴![]() ,
,
且AE=AE,
∴△AEG≌△AEF(SAS),
从而得EG=EF.(全等三角形对应边相等),
又∵BN=DM,BN∥DM,
∴四边形DMBN是平行四边形(一组对边平行且相等的四边形是平行四边形),
∴DN∥BM,
∴![]() (两直线平行,同位角相等),
(两直线平行,同位角相等),
∵![]() ,
,
∴![]() (等量替换),
(等量替换),
即:∠GBE=90°,
则![]() ,
,
∴![]() ;
;
(3)在AB上截取AP,在BC上截取BQ,使AP=AB=BQ=3,连结PQ交AM于点R,
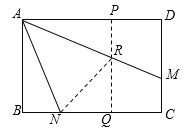
易证ABQP为正方形,
由操作与发现知:PR+BN=RN.
设PR=x,则RQ=3﹣x,RN=1+x,QN=3-1=2
在Rt△QRN中,由勾股定理得:
![]() ,
,
即![]()
解得:x=![]() ,
,
∴PR=![]()
∵PQ∥DC,
∴△APR∽△ADM,
∴![]() (相似三角形对应边成比例)
(相似三角形对应边成比例)
∴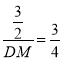
∴DM=2;

【题目】一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利的情况如下表所示:
销售方式 | 粗加工后销售 | 精加工后销售 |
每吨获利(元) | 1000 | 2000 |
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工.
①试求出销售利润![]() 元与精加工的蔬菜吨数
元与精加工的蔬菜吨数![]() 之间的函数关系式;
之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?