题目内容
【题目】综合与实践
问题情境:
已知![]() 是正方形
是正方形![]() 的对角线,将正方形
的对角线,将正方形![]() 和正方形
和正方形![]() 按如图放置.
按如图放置.
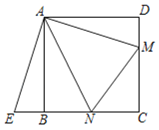
(1)如图1,使点![]() 与点
与点![]() 重合,
重合,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() .求证:
.求证:![]() .
.
操作发现:
图1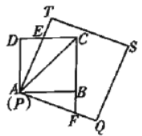
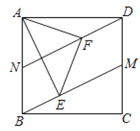
(2)如图2,使点![]() 在
在![]() 上(
上(![]() ,
,![]() 两点除外),
两点除外),![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() .判断
.判断![]() 和
和![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
图2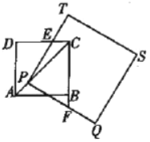
拓广探索:
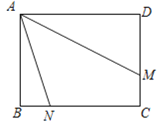
(3)如图3,使![]() 在
在![]() 上(
上(![]() ,
,![]() 两点除外),
两点除外),![]() 经过点
经过点![]() ,
,![]() 与正方形
与正方形![]() 的外角
的外角![]() 的平分线
的平分线![]() 相交于点
相交于点![]() .判断
.判断![]() 和
和![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
图3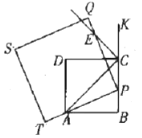
【答案】(1)证明见解析(2)![]() ,理由见解析(3)
,理由见解析(3)![]() ,理由见解析
,理由见解析
【解析】
(1)通正方形得性质得到边角相等来证明![]()
![]()
![]() ,从而得到AF=AE.
,从而得到AF=AE.
(2)过点![]() 作
作![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,与(1)的证明方法一样证明
,与(1)的证明方法一样证明![]()
![]()
![]() ,从而得到PE=PF;
,从而得到PE=PF;
(3)在![]() 上截取
上截取![]() ,连接
,连接![]() .证
.证![]()
![]()
![]() ,从而得到PE=PA.
,从而得到PE=PA.
(1)证明:四边形![]() 为正方形,
为正方形,
![]() ,
,![]() .
.
![]()
又![]() ,
,
![]() .
.
![]() .
.
在![]() 和
和![]() 中,
中,
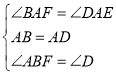 .
.
![]()
![]() .
.
![]() .
.
(2)解:![]() .
.
理由如下:
如答图1,过点![]() 作
作![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,
,
![]() 四边形
四边形![]() 为正方形,
为正方形,
![]() ,
,![]() .
.
![]() ,
,![]() .
.
![]() ,
,![]() .
.
![]() .
.
在![]() 和
和![]() 中,
中,
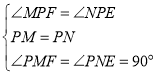
![]()
![]() .
.
![]() .
.
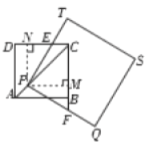
图1
(3)解:![]() .
.
理由如下:
如答图2,在![]() 上截取
上截取![]() ,连接
,连接![]() .
.
![]() 四边形
四边形![]() 为正方形,
为正方形,
![]() ,
,![]() .
.
![]() ,
,![]() .
.
![]() ,
,![]() .
.
![]() 是正方形的外角平分线,
是正方形的外角平分线,
![]() .
.
![]() .
.
![]() ,
,
![]()
又![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,
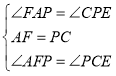
![]()
![]() .
.
![]() .
.
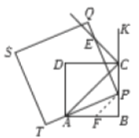
图2

练习册系列答案
相关题目