题目内容
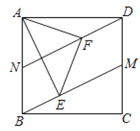
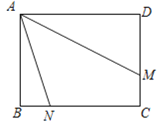
【题目】(1)作图:作∠MON的平分线OE,在OE上任取一点A,过A作AB∥OM,AC∥ON,连接BC交OA于D.(只保留作图痕迹)

(2)BC与OA的位置关系是什么?请加以证明.
(3)若OA=8,AC=5,则BD是多少?
【答案】(1)见解析;(2)BC⊥OA且互相平分,证明见解析;(3)BD=3
【解析】
(1)按要求作图即可得到答案;
(2)先根据平行四边形的判定证明ABCD是·平行四边形,再根据菱形的判定得到ABCD是菱形,由菱形的性质得到BC⊥OA且互相平分;
(3)根据菱形的性质以及勾股定理即可求出BD的长度;
(1)、作图如下

(2)BC⊥OA且互相平分,理由如下:
∵AB∥OM,AC∥ON,
∴四边形ABOC为平行四边形(两组对边分别平行的四边形是平行四边形),
∵AC∥OB
∴∠CAO=∠BOA(两直线平行,内错角相等)
又∵OE平分∠MON,
∴∠COA=∠BOA
∴∠COA=∠CAO
∴AC=OC
∴四边形ABOC为菱形(邻边相等的平行四边形是菱形),
∴BC⊥OA且互相平分;
(3)∵四边形ABOC为菱形
∴AC=OB=5,BC⊥OA,OD=AD=AO=4,
∴![]() ,
,
即25=16+BD2
∴BD2=9
∴BD=3;

 习题精选系列答案
习题精选系列答案【题目】我市某初中课外兴趣活动小组对某水稻品种的稻穗谷粒数目进行调查,从试验田中随机抽取了30株,得到的数据如下(单位:颗):
182 | 195 | 201 | 179 | 208 | 204 | 186 | 192 | 210 | 204 |
175 | 193 | 200 | 203 | 188 | 197 | 212 | 207 | 185 | 206 |
188 | 186 | 198 | 202 | 221 | 199 | 219 | 208 | 187 | 224 |
(1)对抽取的30株水稻稻穗谷粒数进行统计分析,请补全下表中空格,并完善直方图:
谷粒颗数 | 175≤x<185 | 185≤x<195 | 195≤x<205 | 205≤x<215 | 215≤x<225 |
频数 | 8 | 10 | 3 | ||
对应扇形 图中区域 | D | E | C |

(2)如图所示的扇形统计图中,扇形A对应的圆心角为 度,扇形B对应的圆心角为 度;
(3)该试验田中大约有3000株水稻,据此估计,其中稻穗谷粒数大于或等于205颗的水稻有多少株?