题目内容
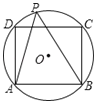
【题目】.如图,点A、B在⊙O上,直线AC是⊙O的切线,OD⊥OB,连接AB交OC于点D.
⑴求证:AC=CD
⑵若AC=2,AO=![]() ,求OD的长度.
,求OD的长度.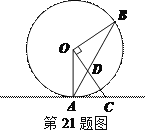
【答案】⑴证明:∵AC是⊙切线,
∴OA⊥AC,
∴∠OAC=90°,
∴∠OAB+∠CAB=90°.
∵OC⊥OB,
∴∠COB=90°,
∴∠ODB+∠B=90°.
∵OA=OB
∴∠OAB=∠B,
∴∠CAB=∠ODB.
∵∠ODB=∠ADC,
∴∠CAB=∠ADC
∴AC=CD.
⑵解:在Rt△OAC中,OC=![]() =3
=3
∴OD=OC-CD=OC-AC=3-2=1
【解析】
试题(1)由AC为圆的切线,利用切线的性质得到∠OAC为直角,再由OC与OB垂直,得到∠BOC为直角,由OA=OB,利用等边对等角得到一对角相等,再利用对顶角相等及等角的余角相等得到一对角相等,利用等角对等边即可得证.
(2)由ODC=OD+DC,DC=AC,表示出OC,在直角三角形OAC中,利用勾股定理即可求出OD的长.
试题解析:(1)∵OA=OB,∴∠OAB=∠B.
∵直线AC为圆O的切线,∴∠OAC=∠OAB+∠DAC=90°.
∵OB⊥OC,∴∠BOC="90°." ∴∠ODB+∠B=90°.
∵∠ODB=∠CDA,∴∠CDA+∠B=90°.
∴∠DAC=∠CDA. ∴AC=CD.
(2)在Rt△OAC中,AC=CD=2,AO=![]() ,OC=OD+DC=OD+2,
,OC=OD+DC=OD+2,
根据勾股定理得:OC2=AC2+AO2,即(OD+2)2=22+(![]() )2,
)2,
解得:OD=1(负值已舍去).

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目