Question

【题目】在一堂数学实践课上，赵老师给出了下列问题：

（提出问题）

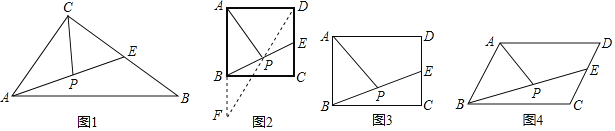
（1）如图1，在△ABC中，E是BC的中点，P是AE的中点，就称CP是△ABC的“双中线”，∠ACB＝90°，AC＝3，AB＝5．则CP＝　 　．

（探究规律）

（2）在图2中，E是正方形ABCD一边上的中点，P是BE上的中点，则称AP是正方形ABCD的“双中线”，若AB＝4．则AP的长为　 　（按图示辅助线求解）；

（3）在图3中，AP是矩形ABCD的“双中线”，若AB＝4，BC＝6，请仿照（2）中的方法求出AP的长，并说明理由；

（拓展应用）

（4）在图4中，AP是平行四边形ABCD的“双中线”，若AB＝4，BC＝10，∠BAD＝120°．求出△ABP的周长，并说明理由？

Answer 1

【答案】（1）；（2）；（3）3；（4）△ABP的周长为4+．

【解析】

（1）利用勾股定理求出AE，再利用直角三角形斜边中线的性质即可解决问题．

（2）利用勾股定理求出DF，再利用直角三角形斜边中线的性质即可解决问题．

（3）如图3中，连接DP，延长DP交AB的延长线于H．利用全等三角形的性质以及勾股定理求出DH即可解决问题．

（4）如图4中，连接DP，延长DP交AB的延长线于H，作DK⊥BA交BA的延长线于K，AN⊥DH于N，EM⊥BC交BC的延长线于M．分别求出BP，AP即可解决问题．

解：（1）如图1中，

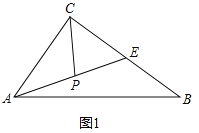
在Rt△ABC中，∵∠ACB＝90°，AB＝5，AC＝3，

∴BC＝

∵E是BC的中点，

∴EC＝EB＝2，

∴AE＝

∵P是AE的中点，

∴PC＝AE＝ ．

故答案为．

（2）如图2中，连接DP，延长DP交AB的延长线于F．

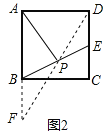
∵四边形ABCD是正方形，

∴AB＝CD＝4，AB∥CD，∠FAD＝90°，

∴∠F＝∠PDE，

∵PB＝PE，∠FPB＝∠EPD，

∴△FPB≌△DPE（AAS），

∴DP＝PF，BF＝DE＝CD＝2，AF＝AB+B4＝2＝6，

在Rt△ADF中，DF＝

∵DP＝PF，

∴AP＝DF＝ ，

故答案为．

（3）如图3中，连接DP，延长DP交AB的延长线于H．

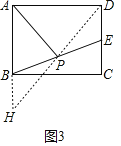
同法可证：∠DAB＝90°，△HPB≌△DPE，

∴DE＝BH＝CD＝2，DP＝PH，AHAB+BH＝6，

在Rt△ADH中，DH＝

∵DP＝PH，

∴PA＝DH＝ ．

（4）如图4中，连接DP，延长DP交AB的延长线于H，作DK⊥BA交BA的延长线于K，AN⊥DH于N，EM⊥BC交BC的延长线于M．

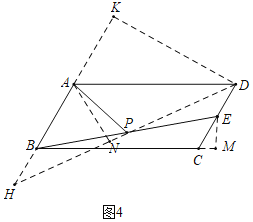
∵四边形ABCD是平行四边形，

∴∠BAD＝∠BCD＝120°，AB＝CD＝4，AD＝BC＝10，

在Rt△ADK中，∵∠KAD＝60°，∠K＝90°，AD＝10，

∴AK＝AD＝5，KD＝AK＝，

在Rt△ECM中，∵∠M＝90°，∠ECM＝60°，EC＝CD＝2，

∴CM＝EC＝1，EM＝ ，

在Rt△BEM中，BE＝

∵P是BE的中点，

∴PB＝EB＝，

∵△PBH≌△PED，

∴DP＝PH，DE＝BH＝2，HK＝BH+AB+AK＝2+4+5＝11，

∴DH＝

∴PH＝PD＝7，

∵∠AHN＝∠DHE，∠ANH＝∠K＝90°，

∴△HAN∽△HDK，

∴

∴

∴AN＝，HN＝，

∴PN＝PH﹣HN＝7﹣＝，

∵AN⊥DH，

∴PA＝

∴△ABP的周长＝AB+PA+PB＝